题目内容
20.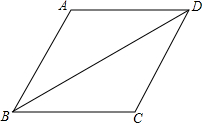 如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.
如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.
分析 根据菱形的周长可以计算菱形的边长,连接AC,菱形的对角线互相垂直平分,已知AB,BO,根据勾股定理即可求得AO的值,进而求出sin∠ABD的值.
解答 解:如图,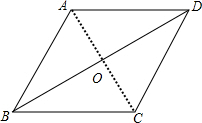
连接AC,交BD于点O,
∵菱形ABCD的周长为20,
∴AB=5,
∵菱形对角线互相垂直平分,
∴BO=4,
∴AO=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴sin∠ABD=$\frac{3}{5}$.
点评 本题考查了菱形对角线互相垂直平分的性质,锐角三角函数的意义,注意菱形各边长相等的性质,勾股定理在直角三角形中的运用,本题中根据勾股定理求AO的值是解题的关键.

练习册系列答案
相关题目
1.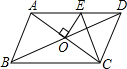 如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
 如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
5.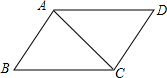 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
 如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )
如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | HL |
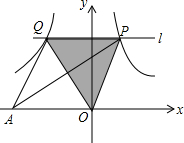 如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=$\frac{6}{x}$(x>0)和y=-$\frac{8}{x}$(x<0)的图象交于点P、Q,连结PO、QO,则△PAQ的面积为7.
如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=$\frac{6}{x}$(x>0)和y=-$\frac{8}{x}$(x<0)的图象交于点P、Q,连结PO、QO,则△PAQ的面积为7.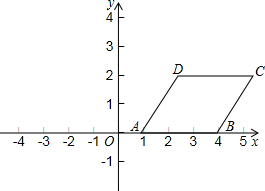 如图,在平面直角坐标系中.?ABCD四个顶点的坐标分别为A(1,0),B(4,0),C(5,2),D(2,2).请你按下列要求画出?ABCD变换后的图形,并写出变换后的图形四个顶点的坐标.
如图,在平面直角坐标系中.?ABCD四个顶点的坐标分别为A(1,0),B(4,0),C(5,2),D(2,2).请你按下列要求画出?ABCD变换后的图形,并写出变换后的图形四个顶点的坐标.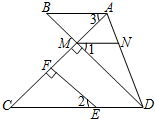 如图,已知EF⊥AC于点F,DB⊥AC于点M,∠1=∠2,∠3=∠C
如图,已知EF⊥AC于点F,DB⊥AC于点M,∠1=∠2,∠3=∠C