题目内容
6.已知正方形有一内切圆,现随意向正方形区域内投掷一点,则此点落在圆内的概率是( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | 1-$\frac{π}{4}$ |
分析 设正方形的边长为a,再用a表示出正方形及圆的面积,根据概率公式即可得出结论.
解答 解:设正方形的边长为a,
∵S正方形=a2,其内切圆的半径为$\frac{a}{2}$,
∴内切圆的面积S圆=πr2=$\frac{π{a}^{2}}{4}$,
∴此点落在圆内的概率=$\frac{{S}_{圆}}{{S}_{正方形}}$=$\frac{\frac{π{a}^{2}}{4}}{{a}^{2}}$=$\frac{π}{4}$.
故选B.
点评 本题考查的是几何概率,熟记概率公式是解答此题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
14.下列命题中真命题是( )
| A. | 有理数都能表示成两个整数之比 | |
| B. | 各边相等的多边形是正多边形 | |
| C. | 等式两边同时乘以(或除以)同一个实数,所得结果仍是等式 | |
| D. | 相等的圆心角所对的弧相等,所对的弦相等 |
1.点A与点B关于x轴对称,点B与点C关于原点对称,若点A的坐标是($\frac{x-a}{|x-a|}$,$\frac{2x-b}{\sqrt{4{x}^{2}-4bx+{b}^{2}}}$)($\frac{b}{2}$<x<a),则点C的坐标是( )
| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
18.已知α为锐角,若tanα=$\frac{1}{2}$,则cosα等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
16.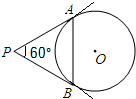 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
 已知如图所示,每个网格中的小正方形的边长都是1,图中的阴影部分是由三段以小正方形的顶点为圆心,半径分别是1和2的圆弧围成,则阴影部分的面积是$\frac{3π}{2}$-3.
已知如图所示,每个网格中的小正方形的边长都是1,图中的阴影部分是由三段以小正方形的顶点为圆心,半径分别是1和2的圆弧围成,则阴影部分的面积是$\frac{3π}{2}$-3.