题目内容
11. 已知如图所示,每个网格中的小正方形的边长都是1,图中的阴影部分是由三段以小正方形的顶点为圆心,半径分别是1和2的圆弧围成,则阴影部分的面积是$\frac{3π}{2}$-3.
已知如图所示,每个网格中的小正方形的边长都是1,图中的阴影部分是由三段以小正方形的顶点为圆心,半径分别是1和2的圆弧围成,则阴影部分的面积是$\frac{3π}{2}$-3.
分析 作出辅助线,运用割补法求出阴影部分的面积即可.
解答  解:作辅助线如图所示:
解:作辅助线如图所示:
阴影部分的面积=$\frac{90π×{2}^{2}}{360}$-$\frac{1}{2}$×2×2+($\frac{90π×{1}^{2}}{360}$-$\frac{1}{2}$×1×1)=$\frac{3π}{2}$-3;
故答案为:$\frac{3π}{2}$-3.
点评 本题考查了正方形的性质、扇形面积的计算;熟练掌握正方形的性质,求出各个扇形面积是解决问题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
19.在△ABC中,∠C=90°,tanA=$\frac{3}{4}$,则sinB,cosB,tanB中最小的是( )
| A. | tanB | B. | sinB | C. | cosB | D. | sinB或cosB |
6.已知正方形有一内切圆,现随意向正方形区域内投掷一点,则此点落在圆内的概率是( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | 1-$\frac{π}{4}$ |
3. 如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )
如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )
 如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )
如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )| A. | $\frac{2ab}{a+b}$ | B. | $\sqrt{ab}$ | C. | $\frac{a+b}{2}$ | D. | $\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ |
1.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | 2+$\sqrt{5}$=2$\sqrt{5}$ | C. | (a2)3=a5 | D. | a2•a2=a4 |
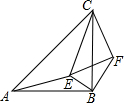 如图,点E在△ABC内,△EFC∽△ABC,∠ABC=∠EFC=90°,∠CAE+∠CBE=90°,连接BF,求证:∠EBF=90°.
如图,点E在△ABC内,△EFC∽△ABC,∠ABC=∠EFC=90°,∠CAE+∠CBE=90°,连接BF,求证:∠EBF=90°.