题目内容
16．
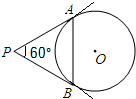如图，从圆O外一点P引圆O的两条切线PA，PB，切点分别为A，B，如果∠APB=60°，PA=8，那么弦AB的长是（ ）| A． | 4 | B． | 4$\sqrt{3}$ | C． | 8 | D． | 8$\sqrt{3}$ |
分析 先利用切线长定理得到PA=PB，再利用∠APB=60°可判断△APB为等边三角形，然后根据等边三角形的性质求解．
解答 解：∵PA，PB为⊙O的切线，
∴PA=PB，
∵∠APB=60°，
∴△APB为等边三角形，
∴AB=PA=8．
故选C．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了切线长定理．
练习册系列答案
相关题目
6．已知正方形有一内切圆，现随意向正方形区域内投掷一点，则此点落在圆内的概率是（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | 1-$\frac{π}{4}$ |
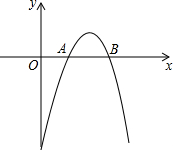如图，二次函数y=-$\frac{1}{2}$x2+bx+c的图象与x轴交于两点A（2，0），B（4，0）
一滴墨水洒在一个数轴上，如图所示，由图中标出的数值，判断墨迹盖住的整数共有多少个？有多少对相反数被盖住呢？
1．下列运算正确的是（ ）
| A． | $\sqrt{4}$=±2 | B． | 2+$\sqrt{5}$=2$\sqrt{5}$ | C． | （a2）3=a5 | D． | a2•a2=a4 |
如图，在△ABC中，∠ACB=90°，AC=6，BC=8，动点D从B出发向A运动，作