题目内容
18．已知α为锐角，若tanα=$\frac{1}{2}$，则cosα等于（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{2\sqrt{5}}{5}$ |
分析 设∠B=α，根据tanα=$\frac{1}{2}$，可设AC=x，BC=2x，由勾股定理求出AB，解直角三角形求出即可．
解答 解：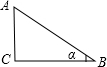
如图，设∠B=α，
∵tanα=$\frac{1}{2}$，
∴$\frac{AC}{BC}$=$\frac{1}{2}$，
设AC=x，BC=2x，
则由勾股定理得：AB=$\sqrt{{x}^{2}+（2x）^{2}}$=$\sqrt{5}$x，
∴cosα=$\frac{BC}{AB}$=$\frac{2x}{\sqrt{5}x}$=$\frac{2\sqrt{5}}{5}$．
故选D．
点评 本题考查了解直角三角形和勾股定理的应用，注意：在Rt△ACB中，∠ACB=90°，则sinA=$\frac{BC}{AB}$，cosA=$\frac{AC}{AB}$，tanA=$\frac{BC}{AC}$．
练习册系列答案
相关题目
6．已知正方形有一内切圆，现随意向正方形区域内投掷一点，则此点落在圆内的概率是（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | 1-$\frac{π}{4}$ |
3．
如图，过圆O直径AB上的点C作AB的垂线交圆O于点D，再过D点作圆的切线l，然后过C点作l的垂线交l于点E，若AC=a，CB=b，那么CE长为（ ）
如图，过圆O直径AB上的点C作AB的垂线交圆O于点D，再过D点作圆的切线l，然后过C点作l的垂线交l于点E，若AC=a，CB=b，那么CE长为（ ）| A． | $\frac{2ab}{a+b}$ | B． | $\sqrt{ab}$ | C． | $\frac{a+b}{2}$ | D． | $\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ |
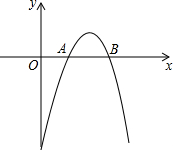如图，二次函数y=-$\frac{1}{2}$x2+bx+c的图象与x轴交于两点A（2，0），B（4，0）
如图，在△ABC中，∠ACB=90°，AC=6，BC=8，动点D从B出发向A运动，作