题目内容
15．先化简，再求值（1）$\frac{a+1}{{a}^{2}-1}$-$\frac{a+1}{1-a}$，其中x=-$\frac{1}{3}$．
（2）（$\frac{3x}{x-2}$$-\frac{x}{x+2}$）$•\frac{{x}^{2}-4}{x}$，其中x=2．
分析 （1）先通分，再根据同分母的分式进行加减即可；
（2）先因式分解，再根据乘法的分配律进行计算即可．
解答 解：（1）原式=$\frac{1}{a-1}$+$\frac{a+1}{a-1}$
=$\frac{1+a+1}{a-1}$
=$\frac{a+2}{a-1}$，
当a=-$\frac{1}{3}$时，原式=$\frac{a+2}{a-1}$
=$\frac{-\frac{1}{3}+2}{-\frac{1}{3}-1}$
=-$\frac{5}{4}$；
（2）原式=$\frac{3x}{x-2}$$•\frac{{x}^{2}-4}{x}$$-\frac{x}{x+2}$$•\frac{{x}^{2}-4}{x}$，
=3（x+2）-（x-2），
=3x+6-x+2
=2x+8，
当x=2时，原式=2x+8=2×2+8=12．
点评 本题考查了分式的化简求值，掌握因式分解以及约分、通分是解题的关键．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
6．已知正方形有一内切圆，现随意向正方形区域内投掷一点，则此点落在圆内的概率是（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | 1-$\frac{π}{4}$ |
3．
如图，过圆O直径AB上的点C作AB的垂线交圆O于点D，再过D点作圆的切线l，然后过C点作l的垂线交l于点E，若AC=a，CB=b，那么CE长为（ ）
如图，过圆O直径AB上的点C作AB的垂线交圆O于点D，再过D点作圆的切线l，然后过C点作l的垂线交l于点E，若AC=a，CB=b，那么CE长为（ ）| A． | $\frac{2ab}{a+b}$ | B． | $\sqrt{ab}$ | C． | $\frac{a+b}{2}$ | D． | $\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ |
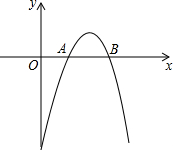如图，二次函数y=-$\frac{1}{2}$x2+bx+c的图象与x轴交于两点A（2，0），B（4，0）
一滴墨水洒在一个数轴上，如图所示，由图中标出的数值，判断墨迹盖住的整数共有多少个？有多少对相反数被盖住呢？