题目内容
14.下列命题中真命题是( )| A. | 有理数都能表示成两个整数之比 | |
| B. | 各边相等的多边形是正多边形 | |
| C. | 等式两边同时乘以(或除以)同一个实数,所得结果仍是等式 | |
| D. | 相等的圆心角所对的弧相等,所对的弦相等 |
分析 分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
解答 解:A、有理数包括整数和分数,整数可以表示为整数:1的形式,分数本身就是分子:分母的形式,故本选项正确;
B、各边都相等,各角都相等的多边形是正多边形,故本选项错误;
C、等式两边同时乘以(或除以)同一个实数(除数不为0),所得结果仍是等式,故本选项正确;
D、在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,故本选项错误;
故选A.
点评 本题考查了判断命题的真假,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
相关题目
19.在△ABC中,∠C=90°,tanA=$\frac{3}{4}$,则sinB,cosB,tanB中最小的是( )
| A. | tanB | B. | sinB | C. | cosB | D. | sinB或cosB |
6.已知正方形有一内切圆,现随意向正方形区域内投掷一点,则此点落在圆内的概率是( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | 1-$\frac{π}{4}$ |
3. 如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )
如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )
 如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )
如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )| A. | $\frac{2ab}{a+b}$ | B. | $\sqrt{ab}$ | C. | $\frac{a+b}{2}$ | D. | $\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ |
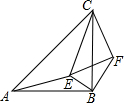 如图,点E在△ABC内,△EFC∽△ABC,∠ABC=∠EFC=90°,∠CAE+∠CBE=90°,连接BF,求证:∠EBF=90°.
如图,点E在△ABC内,△EFC∽△ABC,∠ABC=∠EFC=90°,∠CAE+∠CBE=90°,连接BF,求证:∠EBF=90°. 一滴墨水洒在一个数轴上,如图所示,由图中标出的数值,判断墨迹盖住的整数共有多少个?有多少对相反数被盖住呢?
一滴墨水洒在一个数轴上,如图所示,由图中标出的数值,判断墨迹盖住的整数共有多少个?有多少对相反数被盖住呢?