题目内容
1.点A与点B关于x轴对称,点B与点C关于原点对称,若点A的坐标是($\frac{x-a}{|x-a|}$,$\frac{2x-b}{\sqrt{4{x}^{2}-4bx+{b}^{2}}}$)($\frac{b}{2}$<x<a),则点C的坐标是( )| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
分析 根据x的取值范围确定出x-a与2x-b的正负情况,然后求出点A的坐标,再根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”求出点B的坐标,然后根据“关于原点对称的点,横坐标与纵坐标都互为相反数”求出点C的坐标即可.
解答 解:∵$\frac{b}{2}$<x<a,
∴x-a<0,2x-b>0,
∴$\frac{x-a}{|x-a|}$=-1,$\frac{2x-b}{\sqrt{4{x}^{2}-4bx+{b}^{2}}}$=$\frac{2x-b}{\sqrt{(2x-b)^{2}}}$=$\frac{2x-b}{2x-b}$=1,
∴点A的坐标为(-1,1),
∵点A与点B关于x轴对称,
∴点B的坐标为(-1,-1),
∵点B与点C关于原点对称,
∴点C的坐标为(1,1).
故选D.
点评 本题考查了关于原点对称的点的坐标,关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
16.某校九年级共有1100名学生参加“二诊”考试,随机抽取50名学生进行总成绩统计,其中有20名学生总成绩达到优秀,估计这次“二诊”考试总成绩达到优秀的人数大约为( )
| A. | 400 | B. | 420 | C. | 440 | D. | 460 |
6.已知正方形有一内切圆,现随意向正方形区域内投掷一点,则此点落在圆内的概率是( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | 1-$\frac{π}{4}$ |
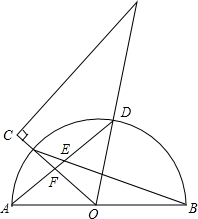 如图,半圆O中,将一块含60°的直角三角板的60°角顶点与圆心O重合,角的两条边分别与半圆圆弧交于C,D两点(点C在∠AOD内部),AD与BC交于点E,AD与OC交于点F.
如图,半圆O中,将一块含60°的直角三角板的60°角顶点与圆心O重合,角的两条边分别与半圆圆弧交于C,D两点(点C在∠AOD内部),AD与BC交于点E,AD与OC交于点F.