题目内容
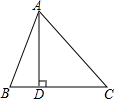 (1)如图,已知AB=13,BC=14,AC=15,AD⊥BC于D,求AD长.
(1)如图,已知AB=13,BC=14,AC=15,AD⊥BC于D,求AD长.(2)已知△ABC中,AB=13,AC=15,AD⊥BC,且AD=12,求BC的长.
考点:勾股定理
专题:
分析:(1)由题意知,BD+DC=14,设BD=x,则CD=14-x,在直角△ABD中,AB是斜边,根据勾股定理AB2=AD2+BD2,在直角△ACD中,根据勾股定理AC2=AD2+CD2,列出方程组即可计算x的值,即可求得AD的长度.
(2)分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CD-BD,问题得解.
(2)分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CD-BD,问题得解.
解答:解:(1)BC=14,且BC=BD+DC,
设BD=x,则DC=14-x,
则在直角△ABD中,AB2=AD2+BD2,
即132=AD2+x2,
在直角△ACD中,AC2=AD2+CD2,
即152=AD2+(14-x)2,
整理计算得x=5,
即AD=12.
(2)①如图,锐角△ABC中,AB=13,AC=15,BC边上高AD=12,
在Rt△ABD中AB=13,AD=12,由勾股定理得
BD2=AB2-AD2=132-122=25,
即BD=5,
在Rt△ABD中AC=15,AD=12,由勾股定理得
CD2=AC2-AD2=152-122=81,
即CD=9,
所以BC的长为BD+DC=9+5=14,
②钝角△ABC中,AB=13,AC=15,BC边上高AD=12,
在Rt△ABD中AB=13,AD=12,由勾股定理得
BD2=AB2-AD2=132-122=25,
即BD=5,
在Rt△ACD中AC=15,AD=12,由勾股定理得
CD2=AC2-AD2=152-122=81,
所以CD=9,
所以BC=DC-BD=9-5=4.
设BD=x,则DC=14-x,
则在直角△ABD中,AB2=AD2+BD2,
即132=AD2+x2,
在直角△ACD中,AC2=AD2+CD2,
即152=AD2+(14-x)2,
整理计算得x=5,
即AD=12.
(2)①如图,锐角△ABC中,AB=13,AC=15,BC边上高AD=12,

在Rt△ABD中AB=13,AD=12,由勾股定理得
BD2=AB2-AD2=132-122=25,
即BD=5,
在Rt△ABD中AC=15,AD=12,由勾股定理得
CD2=AC2-AD2=152-122=81,
即CD=9,
所以BC的长为BD+DC=9+5=14,
②钝角△ABC中,AB=13,AC=15,BC边上高AD=12,

在Rt△ABD中AB=13,AD=12,由勾股定理得
BD2=AB2-AD2=132-122=25,
即BD=5,
在Rt△ACD中AC=15,AD=12,由勾股定理得
CD2=AC2-AD2=152-122=81,
所以CD=9,
所以BC=DC-BD=9-5=4.
点评:(1)本题考查了勾股定理在直角三角形中的灵活运用,考查了学生的方程思想,本题中设BD=x,并且在直角△ABD和直角△ACD中根据勾股定理计算BD是解题的关键.
(2)本题考查了勾股定理,把三角形斜边转化到直角三角形中用勾股定理解答.
(2)本题考查了勾股定理,把三角形斜边转化到直角三角形中用勾股定理解答.

练习册系列答案
相关题目
已知8x3ym÷28xny2=
y2,那么m、n的值为( )
| 2 |
| 7 |
| A、m=4,n=3 |
| B、m=4,n=1 |
| C、m=2,n=3 |
| D、m=1,n=3 |
菱形的周长为20,两邻角的比为2:1,则一组对边的距离为( )
A、
| ||||
B、
| ||||
C、3
| ||||
D、
|
 如图,在直角坐标系xOy中,△ABC的顶点坐标为A(-8,0),B(3,0),C(0,4).动点P从点A出发,沿着AB以每秒1个单位长度的速度向终点B运动;动点Q从点B出发,沿着射线BC,以每秒1个单位长度的速度运动,当点P到达B时,点Q也停止运动.P,Q两点同时开始运动,设运动时间为t秒.
如图,在直角坐标系xOy中,△ABC的顶点坐标为A(-8,0),B(3,0),C(0,4).动点P从点A出发,沿着AB以每秒1个单位长度的速度向终点B运动;动点Q从点B出发,沿着射线BC,以每秒1个单位长度的速度运动,当点P到达B时,点Q也停止运动.P,Q两点同时开始运动,设运动时间为t秒. 已知:如图,EC=DF,AB=CD,AE=BF.△AEC和△BFD全等吗?为什么?
已知:如图,EC=DF,AB=CD,AE=BF.△AEC和△BFD全等吗?为什么? 已知?ABCD的面积是1,E、F分别是AB、CD上的点,AF与DE交于G,
已知?ABCD的面积是1,E、F分别是AB、CD上的点,AF与DE交于G,