题目内容
 已知:如图,EC=DF,AB=CD,AE=BF.△AEC和△BFD全等吗?为什么?
已知:如图,EC=DF,AB=CD,AE=BF.△AEC和△BFD全等吗?为什么?考点:全等三角形的判定
专题:
分析:根据AB=CD,可得AB+BC=CD+BC,即AC=BD,然后根据EC=DF,AE=BF,可判定△AEC和△BFD全等.
解答:解:全等;
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△AEC和△BFD中,
,
∴△AEC≌△BFD(SSS).
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△AEC和△BFD中,
|
∴△AEC≌△BFD(SSS).
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
下列计算正确的是( )
| A、-3+3=0 | ||
| B、-4-4=0 | ||
C、5÷
| ||
| D、62=12 |
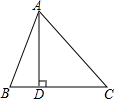 (1)如图,已知AB=13,BC=14,AC=15,AD⊥BC于D,求AD长.
(1)如图,已知AB=13,BC=14,AC=15,AD⊥BC于D,求AD长.