题目内容
已知?ABCD的面积是1，E、F分别是AB、CD上的点，AF与DE交于G，| DF |
| FC |
| b |
| a |
| AE |
| EB |
| d |
| c |
考点：平行四边形的性质
专题：
分析：先由平行四边形的性质得出AB=CD，AB∥CD，那么△AEG∽△FDG，根据相似三角形对应边的比相等得到AG：FG=AE：DF，由已知
=
，
=
，得出DF=
CD，AE=
AB，所以
=
，
=
，再根据?ABCD的面积是1，求出S△ADF=
，进而求出S△DFG．
| DF |
| FC |
| b |
| a |
| AE |
| EB |
| d |
| c |
| b |
| a+b |
| d |
| c+d |
| AG |
| FG |
| d(a+b) |
| b(c+d) |
| FG |
| AF |
| b(c+d) |
| b(c+d)+d(a+b) |
| b |
| 2(a+b) |
解答：解：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴△AEG∽△FDG，
∴AG：FG=AE：DF，
∵
=
，
=
，
∴DF=
CD，AE=
AB，
∴
=
，
∴
=
，
∵?ABCD的面积是1，
∴S△ADF=
，
∴S△DFG=
×
=
．
解：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，
∴△AEG∽△FDG，
∴AG：FG=AE：DF，
∵
| DF |
| FC |
| b |
| a |
| AE |
| EB |
| d |
| c |
∴DF=
| b |
| a+b |
| d |
| c+d |
∴
| AG |
| FG |
| d(a+b) |
| b(c+d) |
∴
| FG |
| AF |
| b(c+d) |
| b(c+d)+d(a+b) |
∵?ABCD的面积是1，
∴S△ADF=
| b |
| 2(a+b) |
∴S△DFG=
| b(c+d) |
| b(c+d)+d(a+b) |
| b |
| 2(a+b) |
| b2(c+d) |
| 2(a+b)[b(c+d)+d(a+b)] |
点评：本题考查了平行四边形的性质，相似三角形的判定与性质，比例的性质，难度适中．求出
=
是解题的关键．
| AG |
| FG |
| d(a+b) |
| b(c+d) |
练习册系列答案
阅读快车系列答案
相关题目
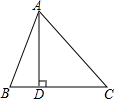（1）如图，已知AB=13，BC=14，AC=15，AD⊥BC于D，求AD长．
如图，直线AB、CD相交于O点，且OA=OB，OC=OD，BD和AC平行吗？为什么？