题目内容
6.已知m、n满足算式(m-6)2+|n-2|=0.(1)求m、n的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=nPB,点Q为PB的中点,求线段AQ的长.
分析 (1)根据非负数的和为零,可得每个非负数同时为零,可得答案;
(2)根据AP=nPB,可得AP的长,根据线段中点的性质,可得PQ的长,根据线段的和差,可得答案.
解答 解:(1)由(m-6)2+|n-2|=0,得
m-6=0,n-2=0.
解得m=6,n=2.
(2)由AB=m,在直线AB上取一点P,恰好使AP=nPB,得
AB=6,AP=2PB=2AB=12.
由点Q为PB的中点,得
PQ=BQ=3.
由线段的和差,得
AQ=AP=PQ=12-3=9,
AQ的长为9.
点评 本题考查了两点间的距离,利用非负数的和为零得出每个非负数同时为零是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.有一组数据:1,3,4,5,5,则这组数据的平均数,众数,中位数分别是( )
| A. | 3.6,5,5 | B. | 5,5,5 | C. | 3.6,5,4 | D. | 3.6,4,5 |
11.计算b2•(-b3)2的结果是( )
| A. | b8 | B. | b11 | C. | -b8 | D. | -b11 |
15.已知$\sqrt{2x-6}$+|y+2|=0,则A(x,y)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第三象限 |
16.若(a-3)2+|b-6|=0,则以a、b为边长的等腰三角形的周长为( )
| A. | 12 | B. | 15 | C. | 12或15 | D. | 18 |

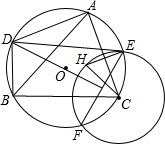 如图,H为△ABC的垂心,圆O为△ABC的外接圆.点E、F为以C为圆心、CH长为半径的圆与圆O的交点,D为线段EF的垂直平分线与圆O的交点.求证:
如图,H为△ABC的垂心,圆O为△ABC的外接圆.点E、F为以C为圆心、CH长为半径的圆与圆O的交点,D为线段EF的垂直平分线与圆O的交点.求证: