题目内容
10.先阅读下面的内容,再解决问题,例题:若m2+2mn+2n2-6n+9=0,求m和n的值.
解:∵m2+2mn+2n2-6n+9=0
∴m2+2mn+n2+n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴m+n=0,n-3=0
∴m=-3,n=3
问题:已知a,b,c为正整数且是△ABC的三边长,c是△ABC的最短边,a,b满足a2+b2=12a+8b-52,求c的值.
分析 根据a2+b2=12a+8b-52,可以求得a、b的值,由a,b,c为正整数且是△ABC的三边长,c是△ABC的最短边,可以求得c的值,本题得以解决.
解答 解:∵a2+b2=12a+8b-52
∴a2-12a+b2-8b+52=0
∴(a-6)2+(b-4)2=0
∴a-6=0或b-4=0,
∴a=6,b=4,
又∵a,b,c为正整数且是△ABC的三边长,c是△ABC的最短边,
∴6-4<c≤4,c是正整数,
∴c=3或c=4,
即c的值是3或4.
点评 本题考查配方法的应用、非负数的性质:偶次方,解题的关键是明确题意,明确配方法和三角形三边的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知$\sqrt{2x-6}$+|y+2|=0,则A(x,y)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第三象限 |

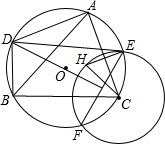 如图,H为△ABC的垂心,圆O为△ABC的外接圆.点E、F为以C为圆心、CH长为半径的圆与圆O的交点,D为线段EF的垂直平分线与圆O的交点.求证:
如图,H为△ABC的垂心,圆O为△ABC的外接圆.点E、F为以C为圆心、CH长为半径的圆与圆O的交点,D为线段EF的垂直平分线与圆O的交点.求证: 如图,在平面直角坐标系中,A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E.已知CD=8,抛物线经过O,E,A三点.
如图,在平面直角坐标系中,A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E.已知CD=8,抛物线经过O,E,A三点.
 如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).
如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).