题目内容
9.(1)解不等式组$\left\{\begin{array}{l}{2x+4≥0}\\{\frac{x-3}{2}+3>x+1}\end{array}\right.$,并写出该不等式组的最大整数解.(2)先化简,再求值:$\frac{a-1}{a}$÷(a-$\frac{2a-1}{a}$),其中a=$\sqrt{2}$+1.
分析 (1)分别求出各不等式的解集,再求出其公共解集,并写出其最大整数解即可;
(2)先算括号里面的,再算除法,最后把a的值代入进行计算即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+4≥0①}\\{\frac{x-3}{2}+3>x+1②}\end{array}\right.$,由①得 x≥-2,由②得x<1,
故不等式组的解集为-2≤x<1,最大整数解为 x=0;
(2)原式=$\frac{a-1}{a}$÷$\frac{{a}^{2}-2a+1}{a}$
=$\frac{a-1}{a}$•$\frac{a}{(a-1)^{2}}$
=$\frac{1}{a-1}$.
当a=$\sqrt{2}$+1时,原式=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
相关题目
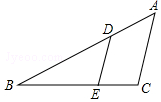 如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BC=5,则EC=$\frac{5}{3}$.
如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BC=5,则EC=$\frac{5}{3}$. 如图,l1∥l2,∠1=35°15′,则∠2的度数为144°45'.
如图,l1∥l2,∠1=35°15′,则∠2的度数为144°45'. 如图:在平行四边形ABCD中,∠DAB的平分线AE交CD于点E,BC=9,AB=15,则CE=6.
如图:在平行四边形ABCD中,∠DAB的平分线AE交CD于点E,BC=9,AB=15,则CE=6.
 填空:
填空: