题目内容
1.解方程组(1)$\left\{\begin{array}{l}{x-3y=5}\\{2x+5y=21}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x-2y=6}\\{2x+3y=17}\end{array}\right.$
(3)$\left\{\begin{array}{l}{x-1=0}\\{2x-y+z=-1}\\{-x+y+z=0}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x-3y=5①}\\{2x+5y=21②}\end{array}\right.$,
由①得:x=3y+5③,
把③代入②得:6y+10+5y=21,即y=1,
把y=1代入③得:x=8,
则方程组的解为$\left\{\begin{array}{l}{x=8}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x-2y=6①}\\{2x+3y=17②}\end{array}\right.$,
①×3+②×2得:13x=52,即x=4,
把x=4代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{x-1=0①}\\{2x-y+z=-1②}\\{-x+y+z=0③}\end{array}\right.$,
由①得:x=1,
②+③得:x+2z=-1,
把x=1代入得:z=-1,
把x=1,z=-1代入③得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,以及三元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
12.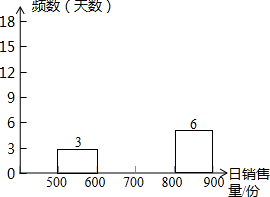 夏季来临,某饮品店老板老李计划下个月(2016年7月)每天制作新鲜水果冰激凌800份销售,去年同期,这种冰激凌每份的成本价为5元,售价为8元,该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失.根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:
夏季来临,某饮品店老板老李计划下个月(2016年7月)每天制作新鲜水果冰激凌800份销售,去年同期,这种冰激凌每份的成本价为5元,售价为8元,该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失.根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:
2015年7月该冰淇淋日销售量频数分布表 2015年7月该冰淇淋日销售量频数分布直方图
由于今年水果涨价,该冰淇淋的制作成本提高了10%.大白计划今年冰淇淋还按8元/份销售.设下个月该冰淇淋的日销售量为m份(0<m≤800).
(1)请根据以上信息补全频数分布表和直方图,并标明相应数据;
(2)用含m的式子表示下个月销售该冰淇淋的日利润;
(3)大白认为,下个月该冰淇淋的销售状况将会与去年同期相差不多.
①请你通过计算帮助大白估计下个月销售该冰淇淋的日利润少于1200元的天数;
②为减少因当日冰淇淋未售出造成的损失,大白计划今年采取下班前打八折销售的方法,希望将剩余的冰淇淋售出.请你通过计算帮助大白估计下个月因销售该冰淇淋获得月利润的范围.
 夏季来临,某饮品店老板老李计划下个月(2016年7月)每天制作新鲜水果冰激凌800份销售,去年同期,这种冰激凌每份的成本价为5元,售价为8元,该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失.根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:
夏季来临,某饮品店老板老李计划下个月(2016年7月)每天制作新鲜水果冰激凌800份销售,去年同期,这种冰激凌每份的成本价为5元,售价为8元,该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失.根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:2015年7月该冰淇淋日销售量频数分布表 2015年7月该冰淇淋日销售量频数分布直方图
| 日销售量分组 | 频数 |
| 500≤x<600 | 3 |
| 600≤x<700 | 6 |
| 700≤x<800 | 16 |
| 800≤x<900 | 6 |
(1)请根据以上信息补全频数分布表和直方图,并标明相应数据;
(2)用含m的式子表示下个月销售该冰淇淋的日利润;
(3)大白认为,下个月该冰淇淋的销售状况将会与去年同期相差不多.
①请你通过计算帮助大白估计下个月销售该冰淇淋的日利润少于1200元的天数;
②为减少因当日冰淇淋未售出造成的损失,大白计划今年采取下班前打八折销售的方法,希望将剩余的冰淇淋售出.请你通过计算帮助大白估计下个月因销售该冰淇淋获得月利润的范围.
13.天津市工信委提供的数据显示,截至去年底,全市光纤入户能力达到6500000户,成为国内首个实现全光纤网络的城市,将6500000用科学记数法表示应为( )
| A. | 0.65×107 | B. | 6.5×106 | C. | 65×105 | D. | 650×104 |
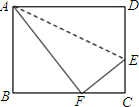 如图,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已AB=32cm,BC=40cm,求CE的长.
如图,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已AB=32cm,BC=40cm,求CE的长.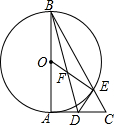 如图,△ABC中.△BAC=90°,以AB为直径作⊙O交BC于E,D为AC的中点,连结DE.
如图,△ABC中.△BAC=90°,以AB为直径作⊙O交BC于E,D为AC的中点,连结DE.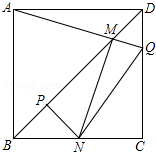 如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.
如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.