题目内容
8.平面上有n个点(n≥2)且任意三个点不在同一直线上,过这些点中的任两点作直线,一共能作出多少条不同的直线?①分析:当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出15条直线.
②归纳:考察点的个数n和可作出直线的条数Sn发现如下表所示:Sn=$\frac{n(n-1)}{2}$.
| 点的个数 | 可连成直线条数 |
| 2 | l=S2=$\frac{2×1}{2}$ |
| 3 | 3=S3=$\frac{3×2}{2}$ |
| 4 | 6=S4=$\frac{4×3}{2}$ |
| 5 | 10=S5=$\frac{5×4}{2}$ |
| … | … |
| n | Sn=$\frac{n(n-1)}{2}$ |
分析 ①根据平面上有n个点,两点确定一条直线.经过第一个点有n-1条直线,过第二个点B有(n-1)条直线,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2,即Sn=$\frac{n(n-1)}{2}$,由此计算得出答案即可;
②根据表中的计算规律直接得出答案即可;
③根据(2)的结论,代入求得答案即可.
解答 解:①当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出$\frac{6×(6-1)}{2}$=15条直线;
②Sn=$\frac{n(n-1)}{2}$;
③当n=2006时,
S2006=$\frac{2006×(2006-1)}{2}$=2011015.
故答案为:15;$\frac{n(n-1)}{2}$;2011015.
点评 此题考查图形的变化规律,观察直线的条数与点的个数之间的关系是解决本题的关键.

练习册系列答案
相关题目
13.问题情境
初次见面,通常以握手示礼,适当的握手时间与力度,会让人有股舒服亲切的感受.9月1日开学时,老师为了让全班新同学互相认识,请班上41位同学彼此握手为礼,并同时彼此介绍自己.在一阵喧哗后,同学完成工作.老师提出一个问题:“谁知道,刚才全班同学总共握手几次?”小聪同学举手抢答说820次,他说的对不对?
探索研究
其实要解决握手问题,可以作以下的分析:假若两点代表两个人,连接两点的线段数目,就表示握手的次数. 我们可以作一个由点和线段组成的图来分析一下
因此,n个人握手总次为P=1+2+3…+(n+1)=$\frac{n(n-1)}{2}$
解决问题
班上41位同学彼此握手为礼,他们共握手多少次?小聪同学说的对不对?
问题拓展
请你用仿照上述方法来研究平面内n条直线最多有多少个交点?请你完成下表:
因此,平面内n条直线最多交点的个数为$\frac{{n({n-1})}}{2}$.
初次见面,通常以握手示礼,适当的握手时间与力度,会让人有股舒服亲切的感受.9月1日开学时,老师为了让全班新同学互相认识,请班上41位同学彼此握手为礼,并同时彼此介绍自己.在一阵喧哗后,同学完成工作.老师提出一个问题:“谁知道,刚才全班同学总共握手几次?”小聪同学举手抢答说820次,他说的对不对?
探索研究
其实要解决握手问题,可以作以下的分析:假若两点代表两个人,连接两点的线段数目,就表示握手的次数. 我们可以作一个由点和线段组成的图来分析一下
| 握手图标 | 握手人数 | 握手次数 |
 | 2 | 1 |
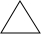 | 3 | 3=1+2 |
 | 4 | 6=1+2+3 |
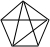 | 5 | 10=1+2+3+4 |
| … | … | … |
| … | N | P=1+2+3+…+(n+1) |
解决问题
班上41位同学彼此握手为礼,他们共握手多少次?小聪同学说的对不对?
问题拓展
请你用仿照上述方法来研究平面内n条直线最多有多少个交点?请你完成下表:
| 图标 | 直线条数 | 交点个数 |
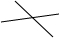 | 2 | 1 |
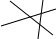 | 3 | 3=1+2 |
 | 4 | |
 | 5 | |
| … | … | … |
| … | n |
18.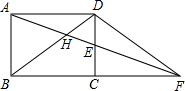 如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )
如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )
 如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )
如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )| A. | $\frac{10\sqrt{6}}{3}$ | B. | 5$\sqrt{2}$ | C. | 10 | D. | 5 |
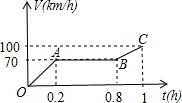 一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:
一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法: …
…