题目内容
7.下列各组数的三个数,可作为三边长构成直角三角形的是( )| A. | 1,2,3 | B. | 32,42,52 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
分析 根据勾股定理的逆定理,只要两边的平方和等于第三边的平方即可构成直角三角形.只要判断两个较小的数的平方和是否等于最大数的平方即可判断.
解答 解:A、∵12+22=5≠32,∴以这三个数为长度的线段不能构成直角三角形,故选项错误;
B、∵(32)2+(42)2≠(52)2 ,∴以这三个数为长度的线段不能构成直角三角形,故选项错误;
C、∵($\sqrt{2}$)2+($\sqrt{3}$)2=5=($\sqrt{5}$)2,∴以这三个数为长度的线段,能构成直角三角形,故选项正确;
D、∵($\sqrt{3}$)2+($\sqrt{4}$)2=7≠($\sqrt{5}$)2,∴以这三个数为长度的线段不能构成直角三角形,故选项错误.
故选:C.
点评 本题主要考查了勾股定理的逆定理,已知三条线段的长,判断是否能构成直角三角形的三边,判断的方法是:判断两个较小的数的平方和是否等于最大数的平方即可判断.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
15. 如图,已知A(3,2),B(5,0),E(4,1),则△AOE的面积为( )
如图,已知A(3,2),B(5,0),E(4,1),则△AOE的面积为( )
 如图,已知A(3,2),B(5,0),E(4,1),则△AOE的面积为( )
如图,已知A(3,2),B(5,0),E(4,1),则△AOE的面积为( )| A. | 5 | B. | 2.5 | C. | 2 | D. | 3 |
12.下列各式中正确的是( )
| A. | $\sqrt{25}$=±5 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | ±$\sqrt{49}$=±7 | D. | $\sqrt{-100}$=10 |
17.已知直线y=kx+8与x轴和y轴所围成的三角形的面积是4,则k的值是( )
| A. | -8 | B. | 8 | C. | ±8 | D. | 4 |
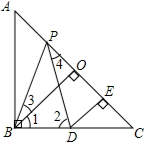 如图,已知在Rt△ABC中,AB=AC,∠ABC=90°,BO⊥AC于点O,点P,D分别在AO和BC上,PB=PD,DE⊥AC于点E;
如图,已知在Rt△ABC中,AB=AC,∠ABC=90°,BO⊥AC于点O,点P,D分别在AO和BC上,PB=PD,DE⊥AC于点E;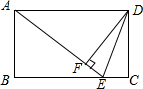 如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.求证:(1)DF=AB;(2)DE是∠FDC的平分线.
如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.求证:(1)DF=AB;(2)DE是∠FDC的平分线.