题目内容
2.计算:(1)-23+$\frac{1}{3}$(2005+3)0-(-$\frac{1}{3}$)-2
(2)tm+1•t+(-t)2•tm(m为整数)
(3)(x-3)(x2-9)(3+x)
(4)(2a-b-3)(2a+b-3)
分析 (1)原式第一项利用乘方的意义计算,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则计算即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,再利用同底数幂的乘法法则计算,合并即可得到结果;
(3)原式结合后,利用平方差公式及完全平方公式计算即可得到结果;
(4)原式利用平方差公式化简,再利用完全平方公式计算即可得到结果.
解答 解:(1)原式=-8+$\frac{1}{3}$-9=-16$\frac{2}{3}$;
(2)原式=tm+2+tm+2=2tm+2;
(3)原式=(x2-9)(x2-9)=x4-18x2+81;
(4)原式=(2a-3)2-b2=4a2-12a-b2+9.
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
10.为了满足市场需求,某厂家生产A、B两种款式的环保购物袋,每天共生产5000个,两种购物袋的成本和售价如下表
设每天生产A种购物袋x个,每天共获利y元
(1)求y与x的函数解析式;
(2)如果该厂每天最多投入成本12000元,那么每天最多获利多少元?
| 成本(元/个) | 售价 (元/个) | |
| A | 2 | 2.4 |
| B | 3 | 3.6 |
(1)求y与x的函数解析式;
(2)如果该厂每天最多投入成本12000元,那么每天最多获利多少元?
7.下列各组数的三个数,可作为三边长构成直角三角形的是( )
| A. | 1,2,3 | B. | 32,42,52 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
14.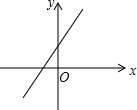 如图是一次函数y=ax-b的图象,则下列判断正确的是( )
如图是一次函数y=ax-b的图象,则下列判断正确的是( )
 如图是一次函数y=ax-b的图象,则下列判断正确的是( )
如图是一次函数y=ax-b的图象,则下列判断正确的是( )| A. | a>0,b<0 | B. | a>0,b>0 | C. | a<0,b<0 | D. | a<0,b>0 |
 正方形ABCD的边AD上有一点E,满足BE=ED+DC,如果M是AD的中点,求证:∠EBC=2∠ABM.
正方形ABCD的边AD上有一点E,满足BE=ED+DC,如果M是AD的中点,求证:∠EBC=2∠ABM. 小明从家骑自行车出发,沿一条直路到相距2400米的移动公司办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局同一条道路步行回家,小明在邮局停留2分钟后沿原路原原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD,线段EF分别表示S1、S2与t之间的函数关系的图象.
小明从家骑自行车出发,沿一条直路到相距2400米的移动公司办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局同一条道路步行回家,小明在邮局停留2分钟后沿原路原原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD,线段EF分别表示S1、S2与t之间的函数关系的图象.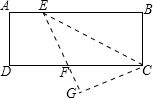 如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.
如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.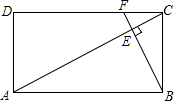 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}$=$\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$.
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}$=$\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$. 如图,点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,若∠BOC=118°,则∠A的角度是56°.
如图,点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,若∠BOC=118°,则∠A的角度是56°.