题目内容
4.在x-2y=5中,(1)用含x的代数式表示y,则y=$\frac{1}{2}$x-$\frac{5}{2}$;
(2)用含y的代数式表示x,则x=2y+5.
分析 (1)要把方程x-2y=5写成用含x的式子表示y的形式,需要把含有y的项移到等号一边,其他的项移到另一边,然后合并同类项、系数化1就可用含x的式子表示y的形式:y=$\frac{1}{2}$x-$\frac{5}{2}$.
(2)把方程x-2y=5写成用含y的式子表示x的形式,把含有x的项移到等号一边,其他的项移到另一边即可.
解答 解:(1)移项得:-2y=5-x
系数化1得:y=$\frac{1}{2}$x-$\frac{5}{2}$.
(2)移项得:x=5+2y
故答案为$\frac{1}{2}$x-$\frac{5}{2}$,2y+5.
点评 本题考查的是方程的基本运算技能:移项、合并同类项、系数化为1等,表示谁就该把谁放到等号的一边,其他的项移到另一边,然后合并同类项、系数化1即可.

练习册系列答案
相关题目
14.如果把分式$\frac{x-y}{xy}$中的x和y都扩大了3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
12.若(a-b-2)2+|a+b+3|=0,则a2-b2的值是( )
| A. | -1 | B. | 1 | C. | 6 | D. | -6 |
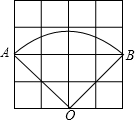 如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).
如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).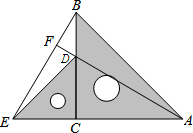 把两个含有45°角的直角三角板如图放置,点D在BC点上,连接BE、AD,AD的延长线交BE于点F,则∠AFB=90°.
把两个含有45°角的直角三角板如图放置,点D在BC点上,连接BE、AD,AD的延长线交BE于点F,则∠AFB=90°.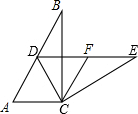 如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.
如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.