题目内容
19.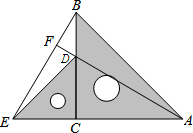 把两个含有45°角的直角三角板如图放置,点D在BC点上,连接BE、AD,AD的延长线交BE于点F,则∠AFB=90°.
把两个含有45°角的直角三角板如图放置,点D在BC点上,连接BE、AD,AD的延长线交BE于点F,则∠AFB=90°.
分析 由SAS可证明△BEC≌△ADC,得出∠EBC=∠DAC,由对顶角相等得出∠FDB=∠CDA,求得∠EBC+∠FDB=90°,即可得出结果.
解答 解:∵△ECD和△BCA都是等腰直角三角形,
∴EC=DC,BC=AC,
∠ECD=∠ACB=90°,
在△BEC和△ADC中,$\left\{\begin{array}{l}{EC=DC}\\{∠ECB=∠DCA}\\{BC=AC}\end{array}\right.$,
∴△BEC≌△ADC(SAS),
∴∠EBC=∠DAC,
∵∠DAC+∠CDA=90°,
∠FDB=∠CDA,
∴∠EBC+∠FDB=90°,
∴∠BFD=90°.
故答案为90.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质;通过证明三角形全等将相等的角进行转换是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
7.过点(-3,2),且平行于x轴的直线上的点( )
| A. | 横坐标都是2 | B. | 纵坐标都是2 | C. | 横坐标都是-3 | D. | 纵坐标都是-3 |
14.若关于x的分式方程$\frac{m}{x-1}$-$\frac{2}{1-x}$=1的解为正数,则m的取值范围是( )
| A. | m>-3 | B. | m≠1 | C. | m>-3且m≠-2 | D. | m>-3且m≠1 |
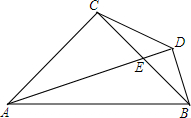 知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.
知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.