题目内容
3.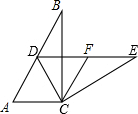 如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.
如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.(1)猜想α与β之间的数量关系,并给予证明;
(2)当α=30°时,点F为DE的中点,判断四边形ACFD的形状,并说明理由.
分析 (1)由直角三角形的性质得出∠A=90°-α,由旋转的性质得出AC=CD,∠ACD=β,由等腰三角形的性质和三角形内角和得出2(90°-α)+β=180°,即可得出结果;
(2)利用直角三角形的性质得出FC=DF,证出△DFC和△ADC是等边三角形,得出AD=AC=FC=DF,即可得出答案.
解答 (1)解:α=$\frac{1}{2}$β;理由如下:
∵∠ACB=90°,∠B=α,
∴∠A=90°-α,
由旋转的性质得:AC=CD,∠ACD=β,
∴∠A=∠ADC=90°-α,
由三角形内角和定理得:2(90°-α)+β=180°,
解得:α=$\frac{1}{2}$β;
(2)解:四边形ACFD是菱形;理由如下:
∵∠DCE=∠ACB=90°,F是DE的中点,
∴FC=DF=FE,
∵∠CDF=∠A=60°,
∴△DFC是等边三角形,
∴DF=DC=FC,
∵△ADC是等边三角形,
∴AD=AC=DC,
∴AD=AC=FC=DF,
∴四边形ACFD是菱形.
点评 本题考查了旋转的性质、等腰三角形的性质、直角三角形的性质、三角形内角和定理、菱形的判定、等边三角形的判定与性质;本题综合性强,难度适中,证明三角形是等边三角形是解决(2)的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
12.比a的$\frac{1}{2}$大5的数是( )
| A. | $\frac{1}{2}$a+5 | B. | a$({\frac{1}{2}+5})$ | C. | $({a+\frac{1}{2}})$+5 | D. | $\frac{1}{2}$(a+5) |
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.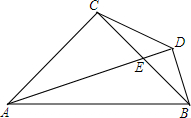 知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.
知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点. 如图,长方形ABCD中,AB=6,CB=8,点P以2个单位/s的速度从A沿AB向B运动,同时点Q以1个单位/s的速度从C沿CB向B运动,当其中的一个点到达终点时,另一个点随之停止运动,设运动时间为t s.
如图,长方形ABCD中,AB=6,CB=8,点P以2个单位/s的速度从A沿AB向B运动,同时点Q以1个单位/s的速度从C沿CB向B运动,当其中的一个点到达终点时,另一个点随之停止运动,设运动时间为t s.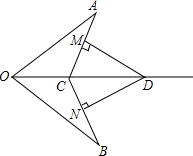 如图,已知C,D在∠AOB的平分线上,OA=OB,DM⊥AC于点M,DN⊥BC于点N.求证:DM=DN.
如图,已知C,D在∠AOB的平分线上,OA=OB,DM⊥AC于点M,DN⊥BC于点N.求证:DM=DN.