题目内容
19.在平面直角坐标系xOy中,反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(-3,m).(1)求反比例函数y1=$\frac{k}{x}$和一次函数y2=ax+b的表达式;
(2)点C 是坐标平面内一点,BC∥x 轴,AD⊥BC 交直线BC 于点D,连接AC.若AC=$\sqrt{5}$CD,求点C的坐标.
分析 (1)由点A在反比例函数图象上,利用待定系数法可求出反比例函数的表达式,由点B在反比例函数图象上,可求出点B的坐标,由点A、B的坐标利用待定系数法即可求出一次函数的表达式;
(2)由BC∥x轴结合点B的坐标可得出点C的纵坐标,再由点A的坐标结合AD⊥BC于点D,即可得出点D的坐标,即得出线段AD的长,在Rt△ADC中,由勾股定理以及线段AC、CD间的关系可求出线段CD的长,再结合点D的坐标即可求出点C的坐标.
解答 解:(1)∵反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(-3,m),
∴点A(1,3)在反比例函数y1=$\frac{k}{x}$的图象上,
∴k=1×3=3,
∴反比例函数的表达式为y1=$\frac{3}{x}$.
∵点B(-3,m)在反比例函数y1=$\frac{3}{x}$的图象上,
∴m=$\frac{3}{-3}$=-1.
∵点A(1,3)和点B(-3,-1)在一次函数y2=ax+b的图象上,
∴$\left\{\begin{array}{l}{a+b=3}\\{-3a+b=-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$.
∴一次函数的表达式为y2=x+2.
(2)依照题意画出图形,如图所示.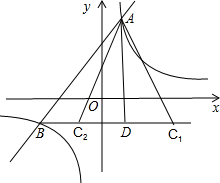
∵BC∥x轴,
∴点C的纵坐标为-1,
∵AD⊥BC于点D,
∴∠ADC=90°.
∵点A的坐标为(1,3),
∴点D的坐标为(1,-1),
∴AD=4,
∵在Rt△ADC中,AC2=AD2+CD2,且AC=$\sqrt{5}$CD,
∴$(\sqrt{5}CD)^{2}={4}^{2}+C{D}^{2}$,解得:CD=2.
∴点C1的坐标为(3,-1),点C2的坐标为(-1,-1).
故点C的坐标为(-1,-1)或(3,-1).
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及解直角三角形,解题的关键是:(1)根据点的坐标利用待定系数法求函数解析式;(2)通过解直角三角形求出线段CD的长.本题属于基础题,难度不大,解决该题型题目时,结合点的坐标利用待定系数法求出函数解析式是关键.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案 如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( )
如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( )| A. | AC=DF | B. | BE=EC | C. | ∠A=∠D | D. | ∠DEF=90° |
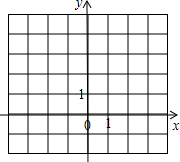 在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).
在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).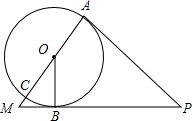 如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.
如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.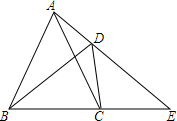 如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:AC•DE=BD•CE.
如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:AC•DE=BD•CE. (1)甲、乙两人用如图所示的①、②两个转盘做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙胜.试求出甲获胜的概率.
(1)甲、乙两人用如图所示的①、②两个转盘做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙胜.试求出甲获胜的概率. 如图,AB是⊙O的直径,D是$\widehat{BC}$的中点,DE⊥AB于E,交CB于点F.过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
如图,AB是⊙O的直径,D是$\widehat{BC}$的中点,DE⊥AB于E,交CB于点F.过点D作BC的平行线DM,连接AC并延长与DM相交于点G.