题目内容
7. 在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).
在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).(1)在坐标系中画出△ABC;
(2)把△ABC绕原点O 顺时针旋转90°得△A′B′C′,画出△A′B′C′;
(3)在(2)的前提下,求△ABC旋转所扫过部分的面积.
分析 (1)根据坐标画出点的位置即可.
(2)根据旋转的条件画出图形即可.
(3)根据△ABC旋转所扫过部分的面积=边AB扫过的面积+△ABC面积=${S}_{扇形OA{A}_{1}}$-${S}_{扇形OB{B}_{1}}$+S△ABC进行计算即可.
解答 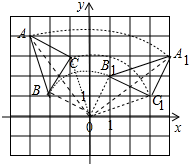 解:(1)△ABC如图所示.
解:(1)△ABC如图所示.
(2)△ABC绕原点O 顺时针旋转90°得△A′B′C′,△A′B′C′如图所示.
(3)△ABC旋转所扫过部分的面积=边AB扫过的面积+△ABC面积
=${S}_{扇形OA{A}_{1}}$-${S}_{扇形OB{B}_{1}}$+S△ABC
=$\frac{90π(5)^{2}}{360}$-$\frac{90π(\sqrt{5})^{2}}{360}$+$\frac{1}{2}$•$\sqrt{5}$•$\sqrt{5}$
=5π+$\frac{5}{2}$.
点评 本题考查作图变换、扇形的面积计算等知识,解题的关键是学会分割法求面积,把不规则图形转化为规则图形考虑,属于中考常考题型.

练习册系列答案
相关题目
18.计算27a8÷$\frac{1}{3}$a3÷9a2的顺序不正确的是( )
| A. | (27÷$\frac{1}{3}$÷9)a8-3-2 | B. | (27a8÷$\frac{1}{3}$a3)÷9a2 | C. | (27a8÷9a2)÷$\frac{1}{3}$a3 | D. | 27a8÷($\frac{1}{3}$a3÷9a2) |
 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.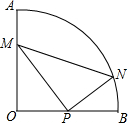 已知:∠AOB=90°,OA=OB=4,P、M、N分别是OB、OA、$\widehat{AB}$上的动点,且∠MPN=90°,PM:PN=3:2,求△PMN周长的最小值.
已知:∠AOB=90°,OA=OB=4,P、M、N分别是OB、OA、$\widehat{AB}$上的动点,且∠MPN=90°,PM:PN=3:2,求△PMN周长的最小值.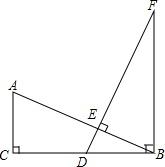 已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF.
已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF. 如图,已知∠ABC=90°,分别以AB和BC为边向外作等边△ABD和等边△BCE,连接AE,CD.
如图,已知∠ABC=90°,分别以AB和BC为边向外作等边△ABD和等边△BCE,连接AE,CD.