题目内容
11．
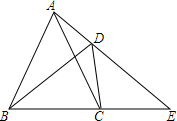如图，已知在四边形ABCD中，∠ADB=∠ACB，延长AD、BC相交于点E．求证：AC•DE=BD•CE．
分析 根据邻补角的定义得到∠BDE=∠ACE，又因为又∠E=∠E，所以可证明△ECA∽△EDB由相似三角形的性质即可得到结论．
解答 证明：∵∠ADB=∠ACB，
∴∠EDB=∠ECA．
又∠E=∠E，
∴△ECA∽△EDB，
∴$\frac{AC}{BD}=\frac{CE}{DE}$，
即AC•DE=BD•CE．
点评 本题考查了相似三角形的判定和性质，邻补角的定义，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
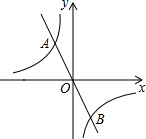如图示，双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A（-1，m）、B（n，-2）两点
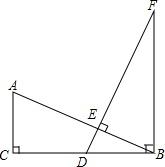已知：如图，在△ABC中，∠ACB=90°，点D在BC上，且BD=AC，过点D作DE⊥AB于点E，过点B作CB的垂线，交DE的延长线于点F．求证：AB=DF．
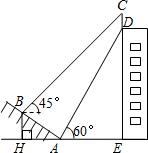如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i=1：$\sqrt{3}$，AB=8米，AE=10米．（i=1：$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比）
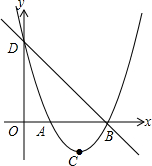如图所示，已知二次函数y=x2-4x+m，它的图象与x轴交于A，B两点（A在B的左侧），与y轴交于点D，且满足OB=OD，顶点为C