题目内容
10.已知等边三角形ABC的面积为18$\sqrt{3}$,若以A为原点,AB为x轴正方向、2cm为单位长度建立平面直角坐标系,则C的坐标为($\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{6}}{2}$)或($\frac{3\sqrt{2}}{2}$,-$\frac{3\sqrt{6}}{2}$).分析 过点C作CD⊥AB于点D,根据等边三角形的性质,设AB=a,则CD=$\frac{\sqrt{3}}{2}$a,结合三角形的面积公式以及三角形ABC的面积为18$\sqrt{3}$,可得出关于a的一元二次方程,解方程即可求出线段AB的长,再根据坐标系的构建方式以及等边三角形的性质即可得出点C的坐标.
解答 解:过点C作CD⊥AB于点D,如图所示.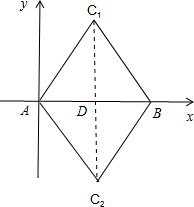
∵△ABC为等边三角形,设AB=a,
则CD=$\frac{\sqrt{3}}{2}$a,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{\sqrt{3}}{4}{a}^{2}$=18$\sqrt{3}$,
解得:a=6$\sqrt{2}$,或a=-6$\sqrt{2}$(舍去).
∵直角坐标系以2cm为单位长度,
∴点B的坐标为(3$\sqrt{2}$,0),
∵△ABC为等边三角形,
∴点C的坐标为($\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{6}}{2}$)或($\frac{3\sqrt{2}}{2}$,-$\frac{3\sqrt{6}}{2}$).
点评 本题考查了等边三角形的性质、坐标与图形的性质以及解一元二次方程,解题的关键是找出点B的坐标.本题属于基础题,难度不大,解决该题型题目时,根据等边三角形的性质结合三角形的面积公式得出等边三角形的边长,再依据坐标系的建立方式找出坐标轴上除原点外的另一顶点坐标是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图,是二次函数y=ax2+bx+c图象的一部分,对称轴为直线x=-1,且过点(-4,0),给出四个结论:①abc<0 ②2a-b=0 ③4a+2b+c<0 ④若点(-6,y1),(3,y2)是该抛物线上的两点,则y1>y2,其中正确的是( )
如图,是二次函数y=ax2+bx+c图象的一部分,对称轴为直线x=-1,且过点(-4,0),给出四个结论:①abc<0 ②2a-b=0 ③4a+2b+c<0 ④若点(-6,y1),(3,y2)是该抛物线上的两点,则y1>y2,其中正确的是( )
 如图,是二次函数y=ax2+bx+c图象的一部分,对称轴为直线x=-1,且过点(-4,0),给出四个结论:①abc<0 ②2a-b=0 ③4a+2b+c<0 ④若点(-6,y1),(3,y2)是该抛物线上的两点,则y1>y2,其中正确的是( )
如图,是二次函数y=ax2+bx+c图象的一部分,对称轴为直线x=-1,且过点(-4,0),给出四个结论:①abc<0 ②2a-b=0 ③4a+2b+c<0 ④若点(-6,y1),(3,y2)是该抛物线上的两点,则y1>y2,其中正确的是( )| A. | ①② | B. | ①②④ | C. | ②③ | D. | ②③④ |
18.计算27a8÷$\frac{1}{3}$a3÷9a2的顺序不正确的是( )
| A. | (27÷$\frac{1}{3}$÷9)a8-3-2 | B. | (27a8÷$\frac{1}{3}$a3)÷9a2 | C. | (27a8÷9a2)÷$\frac{1}{3}$a3 | D. | 27a8÷($\frac{1}{3}$a3÷9a2) |
5. 如图所示,下列条件中,不能得到l1∥l2的是( )
如图所示,下列条件中,不能得到l1∥l2的是( )
 如图所示,下列条件中,不能得到l1∥l2的是( )
如图所示,下列条件中,不能得到l1∥l2的是( )| A. | ∠4=∠5 | B. | ∠1=∠3 | C. | ∠2=∠3 | D. | ∠2+∠4=180° |
 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.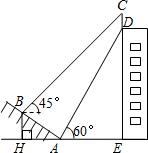 如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:$\sqrt{3}$,AB=8米,AE=10米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)
如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:$\sqrt{3}$,AB=8米,AE=10米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)