题目内容
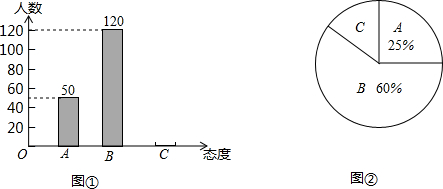
8. (1)甲、乙两人用如图所示的①、②两个转盘做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙胜.试求出甲获胜的概率.
(1)甲、乙两人用如图所示的①、②两个转盘做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙胜.试求出甲获胜的概率.(2)若利用除颜色外其余都相同的红、黄、白色乒乓球各一个设计一个摸球试验,试写出一个与(1)中甲获胜概率相同的事件.(友情提醒:要说明试验的方案,不需说明理由)
分析 (1)列举得出所有等可能的情况数,找出积为奇数的情况数,即可求出甲获胜的概率;
(2)求出甲乙两人获胜的概率,比较即可得到游戏不公平,修改规则即可.
解答 解:
(1)转动两个转盘各1次,所有可能出现的结果有(1,5)、(1,6)、(1,7)、
(2,5)、(2,6)、(2,7)、(3,5)、(3,6)、(3,7),共有9种可能.
它们出现的可能性相同,所有结果中,满足“积为奇数”的结果有4种,
所以转动两个转盘各1次,转出的两个数字之积为奇数的概率为$\frac{4}{9}$.
(2)实验如:在一个不透明的袋子中放入除颜色外其余都相同的红、黄、白色乒乓球各1个,从袋子中取出一个球,记下颜色后放入袋中,再从袋子中取出一个球,记下颜色.事件:两次取出的球中有且只有一个球是红色球.
点评 此题考查了游戏公平性,以及列表法与树状图法,弄清题意是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.计算27a8÷$\frac{1}{3}$a3÷9a2的顺序不正确的是( )
| A. | (27÷$\frac{1}{3}$÷9)a8-3-2 | B. | (27a8÷$\frac{1}{3}$a3)÷9a2 | C. | (27a8÷9a2)÷$\frac{1}{3}$a3 | D. | 27a8÷($\frac{1}{3}$a3÷9a2) |
13.坐标平面内有两点P(x,y),Q(m,n),若x+m=0,y-n=0,则点P与点Q( )
| A. | 关于x轴对称 | B. | 无对称关系 | C. | 关于原点对称 | D. | 关于y轴对称 |
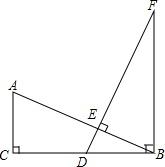 已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF.
已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF.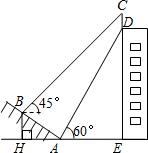 如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:$\sqrt{3}$,AB=8米,AE=10米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)
如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:$\sqrt{3}$,AB=8米,AE=10米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)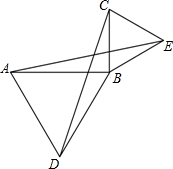 如图,已知∠ABC=90°,分别以AB和BC为边向外作等边△ABD和等边△BCE,连接AE,CD.
如图,已知∠ABC=90°,分别以AB和BC为边向外作等边△ABD和等边△BCE,连接AE,CD.