题目内容
8.已知点A(x1,y1),B(x2,y2)均在直线y=kx+b上,且当x1<x2时,y1>y2,则此直线的函数表达式不可能是( )| A. | y=-2x | B. | y=-2x+1 | C. | y=-$\frac{1}{2}$x-1 | D. | y=$\frac{1}{2}$x-1 |
分析 根据“当x1<x2时,有y1>y2”,可得知一次函数单调递减,由此得出k<0,可做出选择.
解答 解:∵当x1<x2时,有y1>y2,且A(x1,y1),点B(x2,y2)为直线y=kx+b上的点,
∴一次函数y=kx+b单调递减,
∴k<0.
∵A,B,C中的k均小于0,D中的k大于0,
∴D不可能,故选D.
点评 本题考查了一次函数的性质,解题的关键是找出一次函数单调递减.本题属于基础题,难度不大,解决该题型题目时,根据一次函数的性质结合函数的单调性确定k值的取值范围.

练习册系列答案
相关题目
13.解不等式(组)$\left\{\begin{array}{l}{2(1-x)≤x-10}\\{\frac{3x+14}{4}>2x-9}\end{array}\right.$,并写出它的整数解.
20.独山县开展关于精准扶贫、精准扶贫的决策部署以来,某贫困户2014年人均纯收入为2620元,经过帮扶到2016年人均纯收入为3850元,设该贫困户每年纯收入的平均增长率为x,则下面列出的方程中正确的是( )
| A. | 2620(1+x)2=3850 | B. | 2620(1+x)=3850 | C. | 2620(1+2x)=3850 | D. | 2620(1+x)2=3850 |
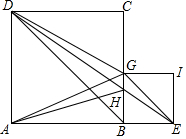 已知正方形ABCD的面积是100,正方形BEFG的面积是25,点H是DE和BC的交点,求△GAH和△GHE的面积之和.
已知正方形ABCD的面积是100,正方形BEFG的面积是25,点H是DE和BC的交点,求△GAH和△GHE的面积之和.
 如图,矩形ABCD中,以AB为直径作⊙O,点E是CD的中点,连接BE交⊙O于点F,连接DF并延长交BC于点G.
如图,矩形ABCD中,以AB为直径作⊙O,点E是CD的中点,连接BE交⊙O于点F,连接DF并延长交BC于点G.