题目内容
9. 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 由角平分线的性质可得AD=DE,∠ABD=∠DBE,由垂直平分线性质可得BD=DC,∠DBE=∠DCE,已知AD,则结合这些信息可以求得AB,BE,CE的长.
解答 解:∵DE是BC的垂直平分线,
∴BD=DC,BE=EC,∠DBE=∠DCE,DE⊥BC,
∵∠ABC的平分线BD交AC于点D,
∴∠ABD=∠DBE,
∵AD⊥AB,DE⊥BE,
∴DE=AD=2,
∵∠BAC=90°,
∴∠DBE=∠DCE=∠ABD=30°,
∴AB=AD•tan30°=2$\sqrt{3}$.
在Rt△ABD和Rt△EBD中
$\left\{\begin{array}{l}{∠A=∠BED}\\{∠ABD=∠DBE}\\{BD=DB}\end{array}\right.$,
∴△ABD≌△EBD(AAS),
即AB=BE,
∴AB=BE=EC=2$\sqrt{3}$.
即图中长为2$\sqrt{3}$的线段有3条.
故选:C.
点评 此题主要考查了角平分线的性质以及全等三角形的判定与性质,正确得出BE=AB是解题关键.

练习册系列答案
相关题目
20. 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )| A. | (3,4)或(2,4) | B. | (2,4)或(8,4) | C. | (3,4)或(8,4) | D. | (3,4)或(2,4)或(8,4) |
17.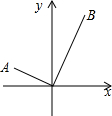 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )| A. | 2$\sqrt{5}$ | B. | 4 | C. | $\sqrt{5}$ | D. | 2 |
1.8月份是新学期开学准备季,东风和百惠两书店对学习用品和工具实施优惠销售.优惠方案分别是:在东风书店购买学习用品或工具书累计花费60元后,超出部分按50%收费;在百惠书店购买学习用品或工具书累计花费50元后,超出部分按60%收费,郝爱同学准备买价值300元的学习用品和工具书,她在哪家书店消费更优惠( )
| A. | 东风 | B. | 百惠 | C. | 两家一样 | D. | 不能确定 |
18.等腰△ABC中,已知有一条边长为4,另一条边长为9,则△ABC的周长为( )
| A. | 13 | B. | 17 | C. | 22 | D. | 17或22 |
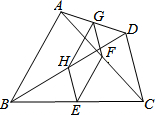 如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是AB=CD.
如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是AB=CD. 如图,在矩形ABCD中,有以下结论:
如图,在矩形ABCD中,有以下结论: 如图AB∥ED,BC∥EF,AF=CD,BE交AD于O
如图AB∥ED,BC∥EF,AF=CD,BE交AD于O