题目内容
4. 如图,在矩形ABCD中,有以下结论:
如图,在矩形ABCD中,有以下结论:①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD.
正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据矩形的性质、正方形的判定方法逐项分析即可
解答 解:∵四边形ABCD是矩形,
∴AO=BO=DO=CO,AC=BD,故①③正确;
∵BO=DO,
∴S△ABO=S△ADO,故②正确;
矩形的对角线相等,但是不一定垂直,故④错误.
故选C
点评 本题考查了矩形的性质、等腰三角形的判定以及正方形的判定,解题的根据是熟记各种特殊几何图形的判定方法和性质.

练习册系列答案
相关题目
15. 如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为( )
如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为( )
 如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为( )
如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为( )| A. | 36° | B. | 44° | C. | 46° | D. | 54° |
19. 如图所示直角梯形的中位线长为a,一腰长为b,此腰与下底所成的夹角为30°,则梯形的面积的表达式为( )
如图所示直角梯形的中位线长为a,一腰长为b,此腰与下底所成的夹角为30°,则梯形的面积的表达式为( )
 如图所示直角梯形的中位线长为a,一腰长为b,此腰与下底所成的夹角为30°,则梯形的面积的表达式为( )
如图所示直角梯形的中位线长为a,一腰长为b,此腰与下底所成的夹角为30°,则梯形的面积的表达式为( )| A. | $\frac{1}{2}$ab | B. | $\frac{1}{3}$ab | C. | $\frac{1}{4}$ab | D. | ab |
9. 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )
 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
14.实数-3,3,0,$\sqrt{2}$中最大的数是( )
| A. | -3 | B. | 3 | C. | 0 | D. | $\sqrt{2}$ |
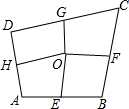 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG=5.
如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG=5.