题目内容
16. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
分析 (1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS得到三角形AEC与三角形ADB全等即可;
(2)根据∠BAC=45°,四边形ADFC是菱形,得到∠DBA=∠BAC=45°,再由AB=AD,得到三角形ABD为等腰直角三角形,求出BD的长,由BD-DF求出BF的长即可.
解答 解:(1)由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,
在△AEC和△ADB中,
$\left\{\begin{array}{l}{AE=AD}\\{∠CAE=∠DAB}\\{AC=AB}\end{array}\right.$,
∴△AEC≌△ADB(SAS);
(2)∵四边形ADFC是菱形,且∠BAC=45°,
∴∠DBA=∠BAC=45°,
由(1)得:AB=AD,
∴∠DBA=∠BDA=45°,
∴△ABD为直角边为2的等腰直角三角形,
∴BD2=2AB2,即BD=2$\sqrt{2}$,
∴AD=DF=FC=AC=AB=2,
∴BF=BD-DF=2$\sqrt{2}$-2.
点评 此题考查了旋转的性质,全等三角形的判定与性质,以及菱形的性质,熟练掌握旋转的性质是解本题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
8.已知反比例函数y=$\frac{6}{x}$,当1<x<3时,y的最小整数值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有13户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是30%;
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%;
(3)家庭用水量的中位数落在C组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分| 分组 | 家庭用水量x/吨 | 家庭数/户 |
| A | 0≤x≤4.0 | 4 |
| B | 4.0<x≤6.5 | 13 |
| C | 6.5<x≤9.0 | |
| D | 9.0<x≤11.5 | |
| E | 11.5<x≤14.0 | 6 |
| F | x>14.0 | 3 |
(1)家庭用水量在4.0<x≤6.5范围内的家庭有13户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是30%;
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%;
(3)家庭用水量的中位数落在C组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
6.一组数据7,8,10,12,13的平均数是( )
| A. | 7 | B. | 9 | C. | 10 | D. | 12 |
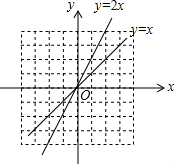 如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变,得到函数y=2x的图象.
如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变,得到函数y=2x的图象.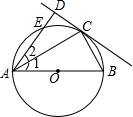 如图,AB为⊙O的直径,点E在⊙O上,C为$\widehat{BE}$的中点,过点C作直线CD⊥AE于D,连接AC、BC.
如图,AB为⊙O的直径,点E在⊙O上,C为$\widehat{BE}$的中点,过点C作直线CD⊥AE于D,连接AC、BC. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.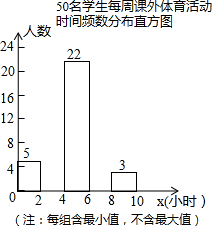 为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题: