题目内容
7.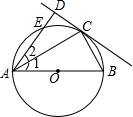 如图,AB为⊙O的直径,点E在⊙O上,C为$\widehat{BE}$的中点,过点C作直线CD⊥AE于D,连接AC、BC.
如图,AB为⊙O的直径,点E在⊙O上,C为$\widehat{BE}$的中点,过点C作直线CD⊥AE于D,连接AC、BC.(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=$\sqrt{6}$,求AB的长.
分析 (1)连接OC,由C为$\widehat{BE}$的中点,得到∠1=∠2,等量代换得到∠2=∠ACO,根据平行线的性质得到OC⊥CD,即可得到结论;
(2)连接CE,由勾股定理得到CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{2}$,根据切割线定理得到CD2=AD•DE,根据勾股定理得到CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\sqrt{3}$,由圆周角定理得到∠ACB=90°,即可得到结论.
解答 解:(1)相切,连接OC,
∵C为$\widehat{BE}$的中点,
∴∠1=∠2,
∵OA=OC,
∴∠1=∠ACO,
∴∠2=∠ACO,
∴AD∥OC,
∵CD⊥AD,
∴OC⊥CD,
∴直线CD与⊙O相切;
(2)方法1:连接CE,
∵AD=2,AC=$\sqrt{6}$,
∵∠ADC=90°,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{2}$,
∵CD是⊙O的切线,
∴CD2=AD•DE,
∴DE=1,
∴CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\sqrt{3}$,
∵C为$\widehat{BE}$的中点,
∴BC=CE=$\sqrt{3}$,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=3.
方法2:∵∠DCA=∠B,
易得△ADC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,
∴AB=3.
点评 本题考查了直线与圆的位置关系,切线的判定和性质,圆周角定理,勾股定理,平行线的性质,切割线定理,熟练掌握各定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{24}$ | C. | $\sqrt{30}$ | D. | $\sqrt{\frac{2}{3}}$ |
2. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A. | a>0 | B. | c<0 | ||
| C. | 3是方程ax2+bx+c=0的一个根 | D. | 当x<1时,y随x的增大而减小 |
19.若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
| A. | x1=0,x2=6 | B. | x1=1,x2=7 | C. | x1=1,x2=-7 | D. | x1=-1,x2=7 |
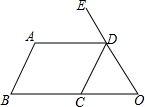 如图,已知AB∥CD,若∠A=110°,∠EDA=60°,则∠CDO=50°.
如图,已知AB∥CD,若∠A=110°,∠EDA=60°,则∠CDO=50°. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.