题目内容
6.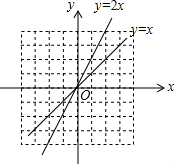 如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变,得到函数y=2x的图象.
如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变,得到函数y=2x的图象.类似地,我们可以认识其他函数.
(1)把函数y=$\frac{1}{x}$的图象上各点的纵坐标变为原来的6倍,横坐标不变,得到函数y=$\frac{6}{x}$的图象;也可以把函数y=$\frac{1}{x}$的图象上各点的横坐标变为原来的6倍,纵坐标不变,得到函数y=$\frac{6}{x}$的图象.
(2)已知下列变化:①向下平移2个单位长度;②向右平移1个单位长度;③向右平移$\frac{1}{2}$个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
(Ⅰ)函数y=x2的图象上所有的点经过④→②→①,得到函数y=4(x-1)2-2的图象;
(Ⅱ)为了得到函数y=-$\frac{1}{4}$(x-1)2-2的图象,可以把函数y=-x2的图象上所有的点D.
A.①→⑤→③B.①→⑥→③C.①→②→⑥D.①→③→⑥
(3)函数y=$\frac{1}{x}$的图象可以经过怎样的变化得到函数y=-$\frac{2x+1}{2x+4}$的图象?(写出一种即可)
分析 (1)根据阅读材料中的规律即可求解;
(2)根据阅读材料中的规律以及“左减右加,上加下减”的规律即可求解;
(3)首先把函数解析式变为y=-$\frac{2x+1}{2x+4}$=$\frac{-2x-4+3}{2x+4}$=$\frac{3}{2(x+2)}$-1,然后根据(2)的规律即可求解.
解答 解:(1)把函数y=$\frac{1}{x}$的图象上各点的纵坐标变为原来的6倍,横坐标不变,
设y′=6y,x′=x,将y=$\frac{y′}{6}$,x=x′带入xy=1可得y′=$\frac{6}{x′}$,得到函数y=$\frac{6}{x}$的图象;
也可以把函数y=$\frac{1}{x}$的图象上各点的横坐标变为原来的6倍,纵坐标不变,
设y′=y,x′=6x,将y=y′,x=$\frac{x′}{6}$代入xy=1可得y′=$\frac{6}{x′}$,得到函数y=$\frac{6}{x}$的图象;
(2)(Ⅰ)函数y=x2的图象上所有的点经过“纵坐标变为原来的4倍,横坐标不变”的变化后,得到y=4x2的图象;y=4x2的图象经过“向右平移1个单位长度”的变化后,得到y=4(x-1)2的图象;y=4(x-1)2的图象经过“向下平移2个单位长度”的变化后,得到y=4(x-1)2-2的图象.
(Ⅱ)为了得到函数y=-$\frac{1}{4}$(x-1)2-2的图象,可以把函数y=-x2的图象上所有的点先向下平移2个单位长度,得到y=-x2-2的图象,再把y=-x2-2的图象向右平移$\frac{1}{2}$个单位长度,得到y=-(x-$\frac{1}{2}$)2-2的图象;最后把y=-(x-$\frac{1}{2}$)2-2的图象的横坐标变为原来的2倍,得到y=-($\frac{1}{2}$x-$\frac{1}{2}$)2-2的图象,即y=-$\frac{1}{4}$(x-1)2-2的图象.
(3)∵y=-$\frac{2x+1}{2x+4}$=$\frac{-2x-4+3}{2x+4}$=$\frac{3}{2(x+2)}$-1,
∴函数y=$\frac{1}{x}$的图象先将纵坐标变为原来的$\frac{3}{2}$倍,横坐标不变,得到y=$\frac{3}{2x}$;再向左平移2个单位,向下平移1个单位即可得到函数y=-$\frac{2x+1}{2x+4}$的图象.
故答案为:(1)6,6;(2)(Ⅰ)y=4(x-1)2-2;(Ⅱ)D.
点评 本题考查图形的平移变换和函数解析式之间的关系.在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.平移后解析式有这样一个规律“左加右减,上加下减”.关键是要搞清楚平移前后的解析式有什么关系.

| A. | 7530(1-x)2=8120 | B. | 7530x2=8120 | C. | 8120(1+x)2=7530 | D. | 7530(1+x)2=8120 |
| A. | $\sqrt{9}$ | B. | $\sqrt{24}$ | C. | $\sqrt{30}$ | D. | $\sqrt{\frac{2}{3}}$ |
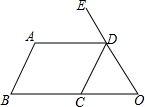 如图,已知AB∥CD,若∠A=110°,∠EDA=60°,则∠CDO=50°.
如图,已知AB∥CD,若∠A=110°,∠EDA=60°,则∠CDO=50°.
 已知一次函数y=2x+4
已知一次函数y=2x+4 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.