题目内容
1.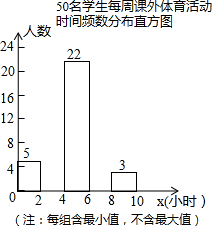 为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:(1)本次调查属于抽样调查,样本容量是50;
(2)请补全频数分布直方图中空缺的部分;
(3)求这50名学生每周课外体育活动时间的平均数;
(4)估计全校学生每周课外体育活动时间不少于6小时的人数.
分析 (1)根据题目中的信息可知本次调查为抽样调查,也可以得到样本容量;
(2)根据每周课外体育活动时间在6≤x<8小时的学生人数占24%,可以求得每周课外体育活动时间在6≤x<8小时的学生人数,从而可以求得2≤x<4的学生数,从而可以将条形统计图补充完整;
(3)根据条形统计图可以得到这50名学生每周课外体育活动时间的平均数;
(4)根据条形统计图,可以估计全校学生每周课外体育活动时间不少于6小时的人数.
解答  解:(1)由题意可得,
解:(1)由题意可得,
本次调查属于抽样调查,样本容量是50,
故答案为:抽样,50;
(2)由题意可得,
每周课外体育活动时间在6≤x<8小时的学生有:50×24%=12(人),
则每周课外体育活动时间在2≤x<4小时的学生有:50-5-22-12-3=8(人),
补全的频数分布直方图如右图所示,
(3)由题意可得,
$\frac{1×5+3×8+5×22+7×12+9×3}{50}$=5,
即这50名学生每周课外体育活动时间的平均数是5;
(4)由题意可得,
全校学生每周课外体育活动时间不少于6小时的学生有:1000×$\frac{12+3}{50}=300$(人),
即全校学生每周课外体育活动时间不少于6小时的学生有300人.
点评 本题考查频数分布直方图、样本、总体、样本容量、用样本估计总体、加权平均数,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
9.已知A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=$\frac{2}{x}$上的三点,若x1<x2<x3,y2<y1<y3,则下列关系式不正确的是( )
| A. | x1•x2<0 | B. | x1•x3<0 | C. | x2•x3<0 | D. | x1+x2<0 |
6.如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )


| A. | 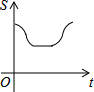 | B. | 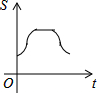 | C. | 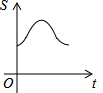 | D. |  |
10.函数y=$\frac{1}{\sqrt{2x-1}}$自变量x的取值范围是( )
| A. | x≤$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
11.若关于x的一元二次方程(k-1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<5 | B. | k<5,且k≠1 | C. | k≤5,且k≠1 | D. | k>5 |
 已知一次函数y=2x+4
已知一次函数y=2x+4 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.