题目内容
8.当 a>1时,方程组$\left\{\begin{array}{l}x+3y={a^2}+a-1\\ 9x-6y=9{a^2}-2a+2\end{array}\right.$的解是正数.分析 根据方程组$\left\{\begin{array}{l}x+3y={a^2}+a-1\\ 9x-6y=9{a^2}-2a+2\end{array}\right.$可以求得方程组的解,又因为方程组$\left\{\begin{array}{l}x+3y={a^2}+a-1\\ 9x-6y=9{a^2}-2a+2\end{array}\right.$的解是正数,从而可以求得a的取值范围.
解答 解:$\left\{\begin{array}{l}{x+3y={a}^{2}+a-1}&{①}\\{9x-6y=9{a}^{2}-2a+2}&{②}\end{array}\right.$
①×2+②,得
x=a2
将x=a2代入①,得
y=$\frac{a-1}{3}$,
∵方程组$\left\{\begin{array}{l}x+3y={a^2}+a-1\\ 9x-6y=9{a^2}-2a+2\end{array}\right.$的解是正数,
∴$\left\{\begin{array}{l}{{a}^{2}>0}\\{\frac{a-1}{3}>0}\end{array}\right.$
解得a>1.
故答案为:>1.
点评 本题考查高次方程,解题的关键是明确题意,找出所求问题需要的条件,会解二元一次方程组.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
19.函数$y=(m+1){x}^{{m}^{2}+m-1}$是反比例函数,则m的值为( )
| A. | 0 | B. | -1 | C. | 0或-1 | D. | 0或1 |
3.若关于x的方程$\frac{x+2}{x-2}+\frac{x-2}{x+2}+\frac{4x+a}{{{x^2}-4}}=0$只有一个实数根,则符合条件的所有实数a的值的总和为( )
| A. | -6 | B. | -30 | C. | -32 | D. | -38 |
20.y是x的反比例函数,下表给出了x与y的一些值:
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表.
| x | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 3 | ||
| y | $\frac{2}{3}$ | 2 | -1 |
(2)根据函数表达式完成上表.
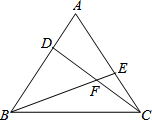 如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.
如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.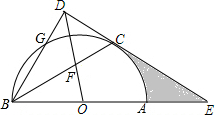 如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F. 用4个小立方体搭成如图摆放的几何体,下面视图是几何体主视图的是( )
用4个小立方体搭成如图摆放的几何体,下面视图是几何体主视图的是( )


