题目内容
某车间有44人,生产一种桌子,每人每天平均生产桌面20个或桌子腿30个,如何分配工人,正好使一天生产的桌面桌腿配套?
考点:一元一次方程的应用
专题:
分析:设出未知数,根据等量关系:桌子腿的总数量=4×桌子面的总数量,列出方程即可解决问题.
解答:解:设λ人生产桌面,(44-λ)人生产桌子腿,
正好使一天生产的桌面桌腿配套;
由题意得:30(44-λ)=4×20λ,
解得:λ=12,44-λ=32;
即12人生产桌面,32人生产桌子腿,正好使一天生产的桌面桌腿配套.
正好使一天生产的桌面桌腿配套;
由题意得:30(44-λ)=4×20λ,
解得:λ=12,44-λ=32;
即12人生产桌面,32人生产桌子腿,正好使一天生产的桌面桌腿配套.
点评:该题主要考查了一元一次方程在现实生活中的应用问题;解题的关键是深入把握题意,准确找出命题中隐含的等量关系,正确列出方程来求解.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=10,AB=8,则⊙O的半径为( )
如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=10,AB=8,则⊙O的半径为( )A、
| ||
B、
| ||
| C、5 | ||
| D、6 |
已知点A和点B在同一数轴上,点A表示数2,又已知点B和点A相距5个单位长度,则点B表示的数是( )
| A、3 |
| B、-7 |
| C、3 或-7 |
| D、-3 或 7 |
 如图,在△ABC中,BP、CP分别是△ABC的外角∠DBC和∠EBC的平分线,试探究∠BPC与∠A的关系.
如图,在△ABC中,BP、CP分别是△ABC的外角∠DBC和∠EBC的平分线,试探究∠BPC与∠A的关系.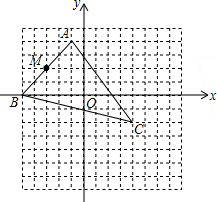 如图,△ABC在平面直角坐标系中,点M在AB上,点A,B,C,O,M均在网格的格点上.
如图,△ABC在平面直角坐标系中,点M在AB上,点A,B,C,O,M均在网格的格点上.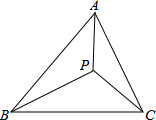 如图,P为△ABC中任意一点.证明:AB+BC+CA>PA+PB+PC.
如图,P为△ABC中任意一点.证明:AB+BC+CA>PA+PB+PC.