题目内容
阅读下列材料,并解决有关问题.
我们知道|x|=
,现在我们可以用这一结论来化简含有绝对值的代数式,如,化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=O,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值).零点值x=-1和x=2可将数轴上的数分成不重复且不遗漏的如下3种情况:
①x<-1;②-1≤x<2;③x≥2.从而化简代数式|x+1|+|x-2|可分以下3种情况:
(1)当x<-1时,原式=-(x+1)-(x-2)=-2x+1;
(2)当-1≤x<2时,原式=x+1-(x-2)=3;
(3)当x≥2时,原式=(x+1)+(x-2)=2x-1.
综上讨论,原式=
.
通过以上阅读,请你解决以下问题:
(1)分别求出|x+2|和|x-4|的零点值;
(2)化简代数式|x+2|+|x-4|.
我们知道|x|=
|
①x<-1;②-1≤x<2;③x≥2.从而化简代数式|x+1|+|x-2|可分以下3种情况:
(1)当x<-1时,原式=-(x+1)-(x-2)=-2x+1;
(2)当-1≤x<2时,原式=x+1-(x-2)=3;
(3)当x≥2时,原式=(x+1)+(x-2)=2x-1.
综上讨论,原式=
|
通过以上阅读,请你解决以下问题:
(1)分别求出|x+2|和|x-4|的零点值;
(2)化简代数式|x+2|+|x-4|.
考点:绝对值
专题:
分析:(1)根据题中所给材料,求出零点值;
(2)将全体实数分成不重复且不遗漏的三种情况解答.
(2)将全体实数分成不重复且不遗漏的三种情况解答.
解答:解:(1)∵|x+2|和|x-4|的零点值,可令x+2=0和x-4=0,解得x=-2和x=4,
∴-2,4分别为|x+2|和|x-4|的零点值.
(2)当x<-2时,|x+2|+|x-4|=-2x+2;
当-2≤x<4时,|x+2|+|x-4|=6;
当x≥4时,|x+2|+|x-4|=2x-2.
∴-2,4分别为|x+2|和|x-4|的零点值.
(2)当x<-2时,|x+2|+|x-4|=-2x+2;
当-2≤x<4时,|x+2|+|x-4|=6;
当x≥4时,|x+2|+|x-4|=2x-2.
点评:本题主要考查了绝对,解题的关键是能根据材料所给信息,找到合适的方法解答.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
下列命题中,错误的是( )
| A、三角形两边之差小于第三边 |
| B、三角形的外角和是360° |
| C、三角形的一边中线能将三角形分成面积相等的两部分 |
| D、正多边形都是中心对称图形 |
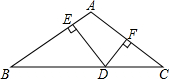 在△ABC中,AB=AC,∠BAC=120°,点D是BC上一动点(不与B、C重合),过点D作DE⊥AB,DF⊥AC.
在△ABC中,AB=AC,∠BAC=120°,点D是BC上一动点(不与B、C重合),过点D作DE⊥AB,DF⊥AC. 已知线段AB=28cm,C是AB上一点,且AC=18cm,O为AB中点,求线段OC的长度.
已知线段AB=28cm,C是AB上一点,且AC=18cm,O为AB中点,求线段OC的长度. 如图,已知AB∥CD∥EF,DG平分∠ADE,若∠BAD=35°,∠CDG=14°,求∠DEF的度数.
如图,已知AB∥CD∥EF,DG平分∠ADE,若∠BAD=35°,∠CDG=14°,求∠DEF的度数.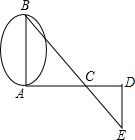 在一次数学活动课上,为了测量河宽AB,其同学采用了如下方法:如图,从A处沿与AB垂直的直线方向走40m到达C处,插一杞标杆,然后沿同方向继续走20m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上,测得DE=30m,这样就可以求出河宽AB,请你算出结果.
在一次数学活动课上,为了测量河宽AB,其同学采用了如下方法:如图,从A处沿与AB垂直的直线方向走40m到达C处,插一杞标杆,然后沿同方向继续走20m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上,测得DE=30m,这样就可以求出河宽AB,请你算出结果. 已知:A(2,4)、B(2,0),通过原点的直线把△AOB的面积分为1:2的两部分,求这条直线的解析式.
已知:A(2,4)、B(2,0),通过原点的直线把△AOB的面积分为1:2的两部分,求这条直线的解析式.