题目内容
8.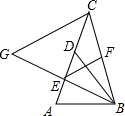 在△ABC中,点D在边AC上,BD=BA,点E是AD的中点,点F是BC的中点.
在△ABC中,点D在边AC上,BD=BA,点E是AD的中点,点F是BC的中点.(1)求证:EF=$\frac{1}{2}$BC;
(2)过点C作CG∥EF,交BE的延长线于G,求证:△BCG是等腰三角形.
分析 (1)由BD=BA,E是AD的中点,根据等腰三角形三线合一的性质得出BE⊥AD,再根据直角三角形斜边上中线等于斜边的一半即可证明EF=$\frac{1}{2}$BC;
(2)先由CG∥EF,根据平行线的性质得出∠G=∠FEB,又EF=$\frac{1}{2}$BC=BF,根据等边对等角得出∠FEB=∠CBE,等量代换得到∠G=∠CBE,那么GC=BC,即△BCG是等腰三角形.
解答 证明:(1)∵BD=BA,E是AD的中点,
∴BE⊥AD,
∴△EBC为直角三角形.
∵F是BC的中点,
∴EF是直角三角形斜边上中线 ∴EF=$\frac{1}{2}$BC;
∴EF=$\frac{1}{2}$BC;
(2)∵CG∥EF,
∴∠G=∠FEB,
∵EF=$\frac{1}{2}$BC=BF,
∴∠FEB=∠CBE,
∴∠G=∠CBE,
∴GC=BC,
∴△BCG是等腰三角形.
点评 本题考查了直角三角形斜边上中线等于斜边的一半的性质,等腰三角形的判定与性质.得出BE⊥AD是证明(1)的关键;得出∠G=∠CBE是证明(2)的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.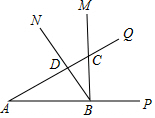 如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
 如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 4 | D. | 12 |
13.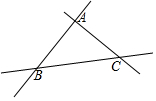 如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )
如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )
 如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )
如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )| A. | △ABC三边的中线的交点上 | B. | △ABC三边垂直平分线的交点上 | ||
| C. | △ABC三条边高的交点上 | D. | △ABC三内角平分线的交点上 |
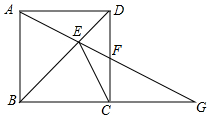 如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.
如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.
 如图,△ABC的顶点坐标分别为A(4,5),B(2,3),C(5,1).
如图,△ABC的顶点坐标分别为A(4,5),B(2,3),C(5,1).