题目内容
上网现在在城市的大多数家庭都是必需的,电信局推出了两种收费方式,用户任选其一:
(1)计时制:0.06元/分;
(2)包月制:50元/月(一户只能一部电话上网),另收电话费0.02元/分.
设某用户4月份上网为x小时,两种收费方式的费用分别为y1(元)、y2(元),写出y1、y2与x之间的函数关系式(不必考虑自变量取值).在上网的时间相同时,哪种方式更省钱?
(1)计时制:0.06元/分;
(2)包月制:50元/月(一户只能一部电话上网),另收电话费0.02元/分.
设某用户4月份上网为x小时,两种收费方式的费用分别为y1(元)、y2(元),写出y1、y2与x之间的函数关系式(不必考虑自变量取值).在上网的时间相同时,哪种方式更省钱?
考点:一次函数的应用
专题:
分析:根据计时制的总价=每分钟的费用×时间就可以表示出出y1,包月制的费用=50元的月租+0.02元/分的电话费×时间就可以得出y2与x之间的函数关系式,再由y1、y2的解析式建立不等式进行分类讨论就可以得出求出结论.
解答:解:由题意,得
y1=0.06x,
y2=0.02x+50.
当y1>y2时,
0.06x>0.02x+50.
解得:x>1250;
当y1=y2时,
0.06x=0.02x+50.
解得:x=1250;
当y1<y2时,
0.06x<0.02x+50.
解得:x<1250;
综上所述,当上网时间超过1250分钟时,包月制优惠些,当上网时间等于1250分钟时两种方式一样优惠,当上网时间少于1250分钟时,计时制优惠些.
y1=0.06x,
y2=0.02x+50.
当y1>y2时,
0.06x>0.02x+50.
解得:x>1250;
当y1=y2时,
0.06x=0.02x+50.
解得:x=1250;
当y1<y2时,
0.06x<0.02x+50.
解得:x<1250;
综上所述,当上网时间超过1250分钟时,包月制优惠些,当上网时间等于1250分钟时两种方式一样优惠,当上网时间少于1250分钟时,计时制优惠些.
点评:本题考查了一次函数的运用,总价=单价×数量的关系的运用,不等式的运用,设计方案的运用,解答时求出一次函数的关系式是关键.

练习册系列答案
相关题目
 如图,AB=12cm,点O自A点以每秒2.5cm的速度沿射线AB方向移动,同时,点E自B点以每秒1cm的速度沿线段BA向A点移动,当E点到达A点时,O、E同时停止运动.已知∠BAM=45°,EF⊥AB交射线AM于点F,以O为圆心,OA长为半径的圆与射线AB、AF分别交于D、C两点,设运动时间为t秒(t>0).
如图,AB=12cm,点O自A点以每秒2.5cm的速度沿射线AB方向移动,同时,点E自B点以每秒1cm的速度沿线段BA向A点移动,当E点到达A点时,O、E同时停止运动.已知∠BAM=45°,EF⊥AB交射线AM于点F,以O为圆心,OA长为半径的圆与射线AB、AF分别交于D、C两点,设运动时间为t秒(t>0). 如图,要测量一幢楼CD的高度,在地面上A点测得楼CD的顶部C的仰角为30°,向楼前进50m到达B点,又测得点C的仰角为60°,求这幢楼CD的高度(结果保留根号)
如图,要测量一幢楼CD的高度,在地面上A点测得楼CD的顶部C的仰角为30°,向楼前进50m到达B点,又测得点C的仰角为60°,求这幢楼CD的高度(结果保留根号) 如图在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,
如图在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm, 已知:(如图)边长为1的正方形ABCD内接于⊙O,点L为劣弧CD(不含端点)上任意一点.直线AL交线段CD于点K,直线CL交直线AD于点M,直线MK交线段BC于点N,线段LB交线段KN于点P.
已知:(如图)边长为1的正方形ABCD内接于⊙O,点L为劣弧CD(不含端点)上任意一点.直线AL交线段CD于点K,直线CL交直线AD于点M,直线MK交线段BC于点N,线段LB交线段KN于点P.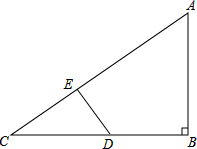 如图,∠B=90°,AB=6,BC=8,DE⊥AC交BC于点D,交AC于点E.设CD的长为x,四边形AEDB面积为y.
如图,∠B=90°,AB=6,BC=8,DE⊥AC交BC于点D,交AC于点E.设CD的长为x,四边形AEDB面积为y.