题目内容
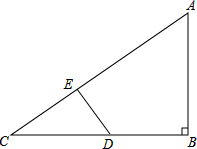如图，∠B=90°，AB=6，BC=8，DE⊥AC交BC于点D，交AC于点E．设CD的长为x，四边形AEDB面积为y．（1）写出y与x的关系式；
（2）当CD为何值时，四边形AEDB的面积为20？
考点：相似三角形的判定与性质,一元二次方程的应用
专题：
分析：（1）运用勾股定理求出AC的长，再利用正弦值求出DE，CE，再利用四边形AEDB面积=△ABC的面积-△CDE的面积，求出y与x的关系式．
（2）令y=20，求出x即可．
（2）令y=20，求出x即可．
解答：解：（1）∵∠B=90°，AB=6，BC=8，
∴AC=
=10，
∴sinC=
=
x，cosC=
=
，
∵CD的长为x，
∴sinC=
=
，cosC=
=
∴DE=
x，CE=
x．
∵四边形AEDB面积=△ABC的面积-△CDE的面积，
∴y=
×6×8-
×
x•
x，即y=24-
x2．
（2）把y=20，代入y=24-
x2得20=24-
x2．
解得x=
．
∴AC=
| AB2+BC2 |
∴sinC=
| AB |
| AC |
| 3 |
| 5 |
| BC |
| AC |
| 4 |
| 5 |
∵CD的长为x，
∴sinC=
| DE |
| CD |
| 3 |
| 5 |
| CE |
| CD |
| 4 |
| 5 |
∴DE=
| 3 |
| 5 |
| 4 |
| 5 |
∵四边形AEDB面积=△ABC的面积-△CDE的面积，
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 6 |
| 25 |
（2）把y=20，代入y=24-
| 6 |
| 25 |
| 6 |
| 25 |
解得x=
10
| ||
| 6 |
点评：本题主要考查了相似三角形的判定与性质及一元二次方程的应用，解题的关键是运用四边形AEDB面积=△ABC的面积-△CDE的面积，求出y与x的关系式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为 （-2，-1），则它们的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
已知：如图，在直角坐标系xOy中，点A（2，0），点B在第一象限且△OAB为正三角形，△OAB的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．