题目内容
 如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正
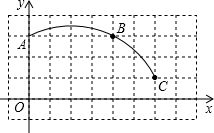
如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正方形边长为1)
(1)请写出该圆弧所在圆的圆心P的坐标
(2)判断点M(-1,2)与⊙P的位置关系,并说明理由;
(3)若点N在⊙P上,且△ABN是直角三角形,直接写出N点坐标.
考点:垂径定理,坐标与图形性质,勾股定理,点与圆的位置关系
专题:
分析:(1)画出P点的位置,即可得出P的坐标,根据勾股定理求出半径即可;
(2)求出MP的长,即可得出答案;
(2)画出符合条件的两种情况,根据A、B的坐标求出即可.
(2)求出MP的长,即可得出答案;
(2)画出符合条件的两种情况,根据A、B的坐标求出即可.
解答:
解:(1)如图,作AB和BC的垂直平分线,交点P就是圆心,即P的坐标是(2,-1),
连接AP,由勾股定理得:AP=
=2
,
故答案为:(2,-1),2
.
(2)在圆内,
理由是:∵P(2,-1),M(-1,2),
∴PM=
=
<2
,
即点M(-1,2)与⊙P的位置关系是在圆内;
(3)如图,

有两种情况:①∠NAB=90°,如N1点,此时N的坐标是(0,-5);
②∠NBA=90°,如N2点,此时N的坐标是(4,-5).

解:(1)如图,作AB和BC的垂直平分线,交点P就是圆心,即P的坐标是(2,-1),
连接AP,由勾股定理得:AP=
| 22+42 |
| 5 |
故答案为:(2,-1),2
| 5 |
(2)在圆内,
理由是:∵P(2,-1),M(-1,2),
∴PM=
| (2+1)2+(-1-2)2 |
| 18 |
| 5 |
即点M(-1,2)与⊙P的位置关系是在圆内;
(3)如图,

有两种情况:①∠NAB=90°,如N1点,此时N的坐标是(0,-5);
②∠NBA=90°,如N2点,此时N的坐标是(4,-5).
点评:本题考查了垂径定理,勾股定理,点和圆的位置关系的应用,主要考查学生的理解能力和计算能力,题目是一道比较好的题目,难度适中.

练习册系列答案
相关题目
若△ABC≌△DEF,则下列说法不正确的是( )
| A、∠A和∠B是对应角 |
| B、AB和DE是对应边 |
| C、点C和点F是对应顶点 |
| D、∠B和∠E是对应角 |
 已知直线y=-3x+6与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c经过点A,B及点M(-4,6).
已知直线y=-3x+6与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c经过点A,B及点M(-4,6).

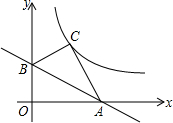 如图,点A(3,0),B(0,
如图,点A(3,0),B(0,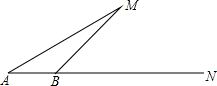 某轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,在小岛M周围120米以内有暗礁,若轮船不改变航向继续前进,有没有触礁的危险?请说明理由.
某轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,在小岛M周围120米以内有暗礁,若轮船不改变航向继续前进,有没有触礁的危险?请说明理由.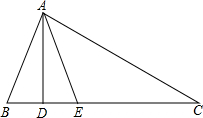 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.