题目内容
如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角尺OMN绕点O按每秒30°的速度沿逆时针方向旋转一周,在旋转的过程中,在第 秒时,边MN恰好与边CD平行;在第 秒时,直线MN恰好与直线CD垂直.(直接写出结果)

(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角尺OMN绕点O按每秒30°的速度沿逆时针方向旋转一周,在旋转的过程中,在第

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据三角形的内角和定理列式计算即可得解;
(2)根据内错角相等,两直线平行判断出MN∥BC,再根据两直线平行,同旁内角互补解答;
(3)作出图形,然后分两种情况求出旋转角,再根据时间=旋转角÷速度计算即可得解.
(2)根据内错角相等,两直线平行判断出MN∥BC,再根据两直线平行,同旁内角互补解答;
(3)作出图形,然后分两种情况求出旋转角,再根据时间=旋转角÷速度计算即可得解.
解答:解:(1)在△CEN中,∠CEN=180°-30°-45°=105°;

(2)∵∠BON=∠N=30°,
∴MN∥BC,
∴∠CEN=180°-∠DCO=180°-45°=135°;
(3)如图,MN∥CD时,旋转角为90°-(60°-45°)=75°,
或270°-(60°-45°)=255°,
所以,t=75°÷30°=2.5秒,
或t=255°÷30°=8.5秒;
MN⊥CD时,旋转角为90°+(180°-60°-45°)=165°,
或360°-(60°-45°)=345°,
所以,t=165°÷30°=5.5秒,
或t=345°÷30°=11.5秒.
故答案为:2.5或8.5;5.5或11.5.

(2)∵∠BON=∠N=30°,
∴MN∥BC,
∴∠CEN=180°-∠DCO=180°-45°=135°;
(3)如图,MN∥CD时,旋转角为90°-(60°-45°)=75°,
或270°-(60°-45°)=255°,
所以,t=75°÷30°=2.5秒,
或t=255°÷30°=8.5秒;
MN⊥CD时,旋转角为90°+(180°-60°-45°)=165°,
或360°-(60°-45°)=345°,
所以,t=165°÷30°=5.5秒,
或t=345°÷30°=11.5秒.
故答案为:2.5或8.5;5.5或11.5.
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,难点在于(3)分情况讨论,作出图形更形象直观.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列运算中,正确的是( )
| A、(a+b)2=a2+b2 | ||||
| B、a3•a4=a12 | ||||
C、
| ||||
D、(
|
用半径为12cm,圆心角为90°的扇形纸片,围成一个圆锥的侧面,这个圆锥的底面半径为( )
| A、12cm | B、6cm |
| C、3cm | D、1.5cm |

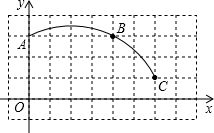 如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正
如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正