题目内容
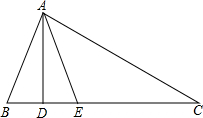 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.(1)求∠BAE的度数;
(2)求∠DAE的度数;
(3)探究:小明认为如果条件中没有“∠B=76°,∠C=26°”,只知道∠B-∠C=50°,也能得出∠DAE的度数.你认为可以吗?若能,请你写出求解过程;若不能,请说明理由.
考点:三角形内角和定理,三角形的外角性质
专题:计算题
分析:(1)根据三角形内角和定理得∠BAC=180°-∠B-∠C=78°,然后根据角平分线定义得∠BAE=
∠BAC=39°;
(2)由于AD⊥BC,则∠ADE=90°,根据三角形外角性质得∠ADE=∠B+∠BAD,所以∠BAD=90°-∠B=14°,然后利用∠DAE=∠BAE-∠BAD进行计算;
(3)根据三角形内角和定理得∠BAC=180°-∠B-∠C,再根据角平分线定义得∠BAE=
∠BAC=
(180°-∠B-∠C)=90°-
(∠B+∠C),加上∠ADE=∠B+∠BAD=90°,则∠BAD=90°-∠B,然后利用角的和差得∠DAE=∠BAE-∠BAD=90°-
(∠B+∠C)-(90°-∠B)=
(∠B-∠C),即∠DAE的度数
等于∠B与∠C差的一半.
| 1 |
| 2 |
(2)由于AD⊥BC,则∠ADE=90°,根据三角形外角性质得∠ADE=∠B+∠BAD,所以∠BAD=90°-∠B=14°,然后利用∠DAE=∠BAE-∠BAD进行计算;
(3)根据三角形内角和定理得∠BAC=180°-∠B-∠C,再根据角平分线定义得∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
等于∠B与∠C差的一半.
解答: 解:(1)∵∠B+∠C+∠BAC=180°,
解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-76°-26°=78°,
∵AE平分∠BAC,
∴∠BAE=
∠BAC=39°;
(2)∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B=90°-76°=14°,
∴∠DAE=∠BAE-∠BAD=39°-14°=35°;
(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=
∠BAC=
(180°-∠B-∠C)=90°-
(∠B+∠C),
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-
(∠B+∠C)-(90°-∠B)=
(∠B-∠C),
∵∠B-∠C=50°,
∴∠DAE=
×50°=25°.
 解:(1)∵∠B+∠C+∠BAC=180°,
解:(1)∵∠B+∠C+∠BAC=180°,∴∠BAC=180°-∠B-∠C=180°-76°-26°=78°,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
(2)∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B=90°-76°=14°,
∴∠DAE=∠BAE-∠BAD=39°-14°=35°;
(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∵∠B-∠C=50°,
∴∠DAE=
| 1 |
| 2 |
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了三角形外角性质.

练习册系列答案
相关题目
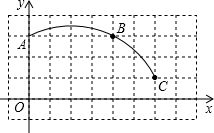 如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正
如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正
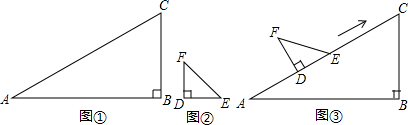
 如图,已知:正方形ABCD,由顶点A引两条射线分别交BC、CD于E、F,且∠EAF=45°,求证:BE+DF=EF.
如图,已知:正方形ABCD,由顶点A引两条射线分别交BC、CD于E、F,且∠EAF=45°,求证:BE+DF=EF. 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若以CEF为顶点的△与以ABC为顶点的三角形相似且AC=3,BC=4时,则AD的长为
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若以CEF为顶点的△与以ABC为顶点的三角形相似且AC=3,BC=4时,则AD的长为