题目内容
如图，将左图中的阴影部分裁剪下来，重新拼成一个如右图的长方形．
（1）根据两个图中阴影部分的面积相等，可以得到一个数学公式 ，这个公式的名称叫 ．
（2）根据你在（1）中得到的公式计算下列算式：（1-
）（1-
）（1-
）（1-
）…（1-
）（1-
）．
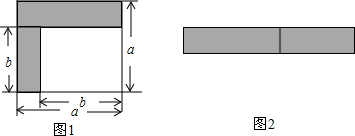
（1）根据两个图中阴影部分的面积相等，可以得到一个数学公式
（2）根据你在（1）中得到的公式计算下列算式：（1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 52 |
| 1 |
| 992 |
| 1 |
| 1002 |
考点：平方差公式的几何背景
专题：
分析：（1）利用面积公式：大正方形的面积-小正方形的面积=阴影面积；利用矩形公式即可求解；利用面积相等列出等式即可；是平方差公式．
（2）利用平方差公式简便计算．
（2）利用平方差公式简便计算．
解答：解：（1）图1的面积为a2-b2，图2的面积为（a+b）（a-b）；比较两图的阴影部分面积，可以得到乘法公式a2-b2=（a+b）（a-b）．
（2）原式=(1-
)(1+
)(1-
)(1+
)…(1-
)(1+
)(1-
)(1+
)
=
×
×
×
×…
×
×
×
=
（2）原式=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 99 |
| 1 |
| 99 |
| 1 |
| 100 |
| 1 |
| 100 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 98 |
| 99 |
| 100 |
| 99 |
| 99 |
| 100 |
| 101 |
| 100 |
=
| 101 |
| 200 |
点评：本题综合考查了证明平方差公式和使用平方差公式的能力．
练习册系列答案
天天练口算系列答案
相关题目
若点（3，6）在反比例函数y=
（k≠0）的图象上，那么下列各点在此图象上的是（ ）
| k |
| x |
| A、（-3，6） |
| B、（2，9） |
| C、（2，-9） |
| D、（3，-6） |
如图是体育委员会对体育活动支持情况的统计，在其他类中对应的百分数为（ ）| A、5% | B、1% |
| C、30% | D、10% |
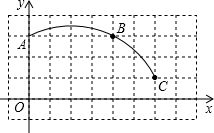如图，在平面直角坐标系中，一段圆弧经过格点A、B、C．（网格小正