先化简.再求值:$\frac{{x}^{2}-1}{{x}^{2}+x}$÷.其中x=$\sqrt{3}$+1．题目和参考答案——青夏教育精英家教网—

题目内容

14．先化简，再求值：$\frac{{x}^{2}-1}{{x}^{2}+x}$÷（x-$\frac{2x-1}{x}$），其中x=$\sqrt{3}$+1．

分析先算括号里面的，再算除法，把分式化为最简分式，把x的值代入进行计算即可．

解答解：原式=$\frac{（x+1）（x-1）}{x（x+1）}$÷$\frac{（x-1）^{2}}{x}$
=$\frac{x-1}{x}$•$\frac{x}{（x-1）^{2}}$
=$\frac{1}{x-1}$，
当x=$\sqrt{3}$+1时，原式=$\frac{1}{\sqrt{3}+1-1}$=$\frac{\sqrt{3}}{3}$．

点评本题考查的是分式的化简求值，分式求值题中比较多的题型主要有三种：转化已知条件后整体代入求值；转化所求问题后将条件整体代入求值；既要转化条件，也要转化问题，然后再代入求值．

练习册系列答案

相关题目

4．

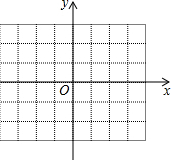如图是一个平面直角坐标系，在坐标系中描出下列各点：A（1，2），B（3，2），C（-1，1），D（-1，-2）．
（1）连接AB、CD，写出线段AB、CD的中点坐标；
（2）观察所得的中点坐标的特征，连按AC，试写出线段AC的中点坐标；
（3）经过测量发现：点A在点C的北偏东63°的方向上，与点C相距约2.2个单位长度，如何用方向和距离描述点C相对于点A的位置？

5．计算$\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}}+\sqrt{1+\frac{1}{2^2}+\frac{1}{3^2}}+\sqrt{1+\frac{1}{3^2}+\frac{1}{4^2}}+…+\sqrt{1+\frac{1}{{{{99}^2}}}+\frac{1}{{{{100}^2}}}}$的值．

2．

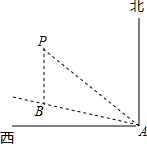如图，一艘船以每小时24海里的速度向北偏西75°方向航行，在点A灯处测得灯塔P在船的西北方向，航行40分钟后到达点B处，这时灯塔P恰好在船的正北方向，已知距离灯塔9海里以外的海区为安全航行区域．问：这艘船能否按原方向继续向前航行？为什么？

9．

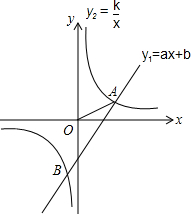如图．点A（3，1），B（-1，n）是一次函数y₁=ax+b和反比例函数y₂=$\frac{k}{x}$图象的交点．
（1）求两个函数的表达式；
（2）观察图象直接写出y₁≥y₂时自变量x的取值范围；
（3）在平面内求点M，使△AOM是以OA为直角边的等腰直角三角形，请你直接写出点M的坐标．

19．

如图，在一块△ABC板面中，将△BEF涂黑，其中点D、E、F分别为BC、AD、CE的中点，小华随意向△ABC板面内部射击一粒小弹丸，则弹丸击中黑色区域的概率是（　　）

6．“掷实心球”是我市初中毕业生体育测试项目之一．测试时，记录下学生掷实心球的成绩，然后按照评分标准转化为相应的分数，满分10分．其中男生掷实心球的评分标准如下：

成绩（米）	…	6.00～6.49	6.50～6.99	7.00～7.49	7.50～7.99	8.00～8.49	8.50及以上
得分（分）	…	5	6	7	8	9	10

某校九年级有500名男生参加掷实心球模拟测试，现从中随机抽取10名男生测试成绩（单位：米）如下：
7.39　8.69　9.41　7.50　8.50　7.89　11.11　8.31　6.09　8.11
请完成下列问题：
（1）求这10名男生掷实心球成绩的平均数；
（2）这10名男生掷实心球得分的众数是10，中位数是9；
（3）如果将9分（含9分）以上定为“优秀”，请你估计这500名男生在这次模拟测试中得优秀的人数．

3．四张卡片，分别标有1，2，3，4四个数字．
（1）从中随机取出一张卡片，请直接写出卡片上数字是奇数的概率$\frac{1}{2}$；
（2）从中随机取出两张卡片，求两张卡片上数字之和大于4的概率．

13．

一只蚂蚁从长为4cm、宽为3cm，高是12cm的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是$\sqrt{193}$．

试题分类