题目内容
5.计算$\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}}+\sqrt{1+\frac{1}{2^2}+\frac{1}{3^2}}+\sqrt{1+\frac{1}{3^2}+\frac{1}{4^2}}+…+\sqrt{1+\frac{1}{{{{99}^2}}}+\frac{1}{{{{100}^2}}}}$的值.分析 直接利用根号下数据规律进而化简求出答案.
解答 解:原式=$\sqrt{\frac{9}{4}}$+$\sqrt{\frac{49}{36}}$+$\sqrt{\frac{169}{144}}$+…+$\sqrt{(\frac{99×100+1}{99×100})^{2}}$
=$\frac{3}{2}$+$\frac{7}{6}$+$\frac{13}{12}$+…+$\frac{99×100+1}{99×100}$
=1×99+(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{99}$-$\frac{1}{100}$)
=99+1-$\frac{1}{100}$
=99$\frac{99}{100}$.
点评 此题主要考查了二次根式的加减运算,正确化简得出数字变化规律是解题关键.

练习册系列答案
相关题目
15.如图(1),B是线段AD上一点,分别以AB、BD为边在AD同侧作等边△ABC和等边△BDE,得到(1)△ABE≌△CBD;(2)AE与CD相交所得的锐角为60°.如图(2),B是线段AE上一点,分别以AB、BE为边在AE同侧作正方形ABCD和正方形BEFG,除了得到△ABG≌△CBE外,AG与CE相交所得的角的度数为( )
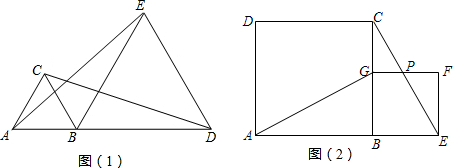

| A. | 90° | B. | 60° | C. | 120° | D. | 不能确定 |
20.y是x的反比例函数,下表给出了x与y的一些值:
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表.
| x | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 3 | ||
| y | $\frac{2}{3}$ | 2 | -1 |
(2)根据函数表达式完成上表.
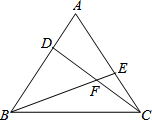 如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.
如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.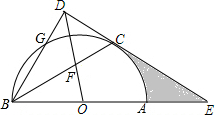 如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.