题目内容
4.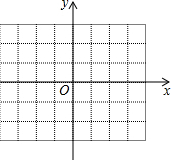 如图是一个平面直角坐标系,在坐标系中描出下列各点:A(1,2),B(3,2),C(-1,1),D(-1,-2).
如图是一个平面直角坐标系,在坐标系中描出下列各点:A(1,2),B(3,2),C(-1,1),D(-1,-2).(1)连接AB、CD,写出线段AB、CD的中点坐标;
(2)观察所得的中点坐标的特征,连按AC,试写出线段AC的中点坐标;
(3)经过测量发现:点A在点C的北偏东63°的方向上,与点C相距约2.2个单位长度,如何用方向和距离描述点C相对于点A的位置?
分析 (1)根据图形和坐标特征容易得出结果;
(2)由(1)得出结论,即可得出结果;
(3)根据方向和距离容易得出结论.
解答 解:(1)如图1所示: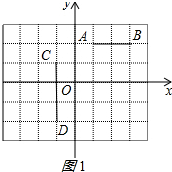
线段AB的中点坐标为(2,2),线段CD的中点的坐标为(-1,-$\frac{1}{2}$);
(2)如图2所示: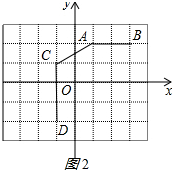
AC的中点坐标为($\frac{1-1}{2}$,$\frac{2+1}{2}$),
即(0,$\frac{3}{2}$);
(3)相对于点A的位置,点C在点A南偏西63°,与点A相距2.2个单位长度.
点评 本题考查了坐标与图形性质、中点坐标的特点以及方向角;根据题意画出图形是解决问题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
15.如图(1),B是线段AD上一点,分别以AB、BD为边在AD同侧作等边△ABC和等边△BDE,得到(1)△ABE≌△CBD;(2)AE与CD相交所得的锐角为60°.如图(2),B是线段AE上一点,分别以AB、BE为边在AE同侧作正方形ABCD和正方形BEFG,除了得到△ABG≌△CBE外,AG与CE相交所得的角的度数为( )
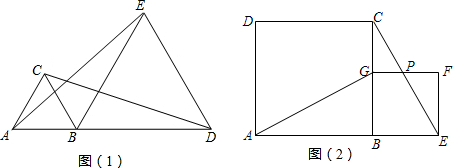

| A. | 90° | B. | 60° | C. | 120° | D. | 不能确定 |
19.函数$y=(m+1){x}^{{m}^{2}+m-1}$是反比例函数,则m的值为( )
| A. | 0 | B. | -1 | C. | 0或-1 | D. | 0或1 |
 不同的中文代表不同的数字,则“中国福州”这个四位数是1098.
不同的中文代表不同的数字,则“中国福州”这个四位数是1098.
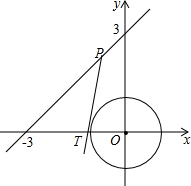 如图,在直角坐标系中,圆O是以坐标原点为圆心,半径为1的圆,直线L的方程为x-y+3=0,在L上任取一点P作圆O的切线,切点为T,则PT长的最小值是$\frac{\sqrt{14}}{2}$.
如图,在直角坐标系中,圆O是以坐标原点为圆心,半径为1的圆,直线L的方程为x-y+3=0,在L上任取一点P作圆O的切线,切点为T,则PT长的最小值是$\frac{\sqrt{14}}{2}$.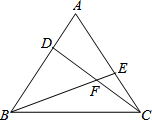 如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.
如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.