题目内容
10.不等式组$\left\{\begin{array}{l}{2x+5≥-1}\\{\frac{x}{3}<\frac{3}{2}}\end{array}\right.$的整数解的和是4,积是0.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,列出所有整数解,再相加、相乘可得结果.
解答 解:解不等式2x+5≥-1,得:x≥-3,
解不等式$\frac{x}{3}<\frac{3}{2}$,得:x<$\frac{9}{2}$,
则原不等式组的解集为:-3≤x<$\frac{9}{2}$,
在此范围内的整数解有:-3,-2,-1,0,1,2,3,4,
故所有整数解的和为:-3+(-2)+(-1)+0+1+2+3+4=4,
所有整数解的积为:(-3)×(-2)×(-1)×0×1×2×3×4=0.
故答案为:4,0.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
2.二元一次方程组$\left\{\begin{array}{l}{x+2y=2}\\{2x+y=-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$ |
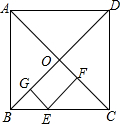 如图,在正方形ABCD中,对角线AC、BD交于O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G、F,AC=10,则EG+EF=5.
如图,在正方形ABCD中,对角线AC、BD交于O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G、F,AC=10,则EG+EF=5.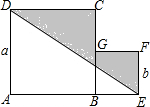 两个边长为a、b的正方形拼成如图所示的形状,连结D、E,求阴影部分的面积.
两个边长为a、b的正方形拼成如图所示的形状,连结D、E,求阴影部分的面积.