题目内容
19.若(x2+px+$\frac{28}{3}$)(x2-3x+q)的展开式中不含x2和x3的项.(1)求p,q的值;
(2)求代数式(-2p2q)3+(3pq)-1+p2014q2016的值.
分析 (1)把首先利用多项式乘多项式法则进而得出原式的展开式的x2项和x3项,进而组成方程组得出p,q的值;
(2)把p,q的值代入代数式即可求得答案.
解答 解:(1)∵(x2+px+$\frac{28}{3}$)(x2-3x+q)
=x4-3x3+qx2+px3-3px2+pqx+$\frac{28}{3}$x2-28x+$\frac{28}{3}$q
=x4+(-3+p)x3+(q-3p+$\frac{28}{3}$)x2+(pq-28)x+$\frac{28}{3}$q,
∴原式的展开式的x2项和x3项分别是(q-3p+$\frac{28}{3}$),(-3+p)x3,
依据题意得:$\left\{\begin{array}{l}{q-3p+\frac{28}{3}=0}\\{-3+p=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{p=3}\\{q=-\frac{1}{3}}\end{array}\right.$.
故p的值是3,q的值是-$\frac{1}{3}$;
(2)(-2p2q)3+(3pq)-1+p2014q2016
=[-2×32×(-$\frac{1}{3}$)]3+[3×3×(-$\frac{1}{3}$)]-1+32014×(-$\frac{1}{3}$)2016
=63+2-1+(-$\frac{1}{3}$)2
=216+$\frac{1}{2}$+$\frac{1}{9}$
=216$\frac{11}{18}$.
点评 此题主要考查了多项式乘多项式,正确展开多项式是解题关键.

练习册系列答案
相关题目
11.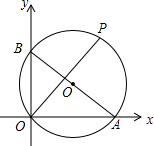 如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
 如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )| A. | (8,6) | B. | (7,7) | C. | (7$\sqrt{2}$,7$\sqrt{2}$) | D. | (5$\sqrt{2}$,5$\sqrt{2}$) |
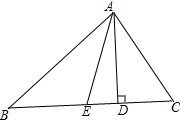 如图,AD、AE分别是△ABC的高、中线,AB=15,BC=14,CA=13.求:
如图,AD、AE分别是△ABC的高、中线,AB=15,BC=14,CA=13.求: 如图,在两个同心圆中,AB、CD分别是大圆和小圆的直径.求证:四边形ACBD是平行四边形.
如图,在两个同心圆中,AB、CD分别是大圆和小圆的直径.求证:四边形ACBD是平行四边形.