题目内容
1.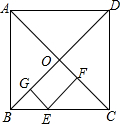 如图,在正方形ABCD中,对角线AC、BD交于O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G、F,AC=10,则EG+EF=5.
如图,在正方形ABCD中,对角线AC、BD交于O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G、F,AC=10,则EG+EF=5.
分析 由S△BOE+S△COE=S△BOC即可解决问题.
解答 解:∵四边形ABCD是正方形,AC=10,
∴AC⊥BD,BO=OC=5,
∵EG⊥OB,EF⊥OC,
∴S△BOE+S△COE=S△BOC,
∴$\frac{1}{2}$•BO•EG+$\frac{1}{2}$•OC•EF=$\frac{1}{2}$•OB•OC,
∴$\frac{1}{2}$×5×EG+$\frac{1}{2}$×5×EF=$\frac{1}{2}$×5×5,
∴EG+EF=5.
故答案为5.
点评 本题考查正方形的性质,利用面积法是解决问题的关键,这里记住一个结论:等腰三角形底边上一点到两腰的距离之和等于腰上的高,填空题可以直接应用,属于中考常考题型.

练习册系列答案
相关题目
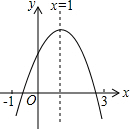 已知二次函数y=ax2+bx+c(a≠0)图象如图,有下列8个结论:
已知二次函数y=ax2+bx+c(a≠0)图象如图,有下列8个结论: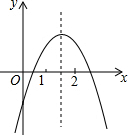 一次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;
一次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;