题目内容
13.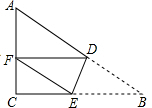 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )| A. | $\frac{40}{9}$ | B. | $\frac{50}{9}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |
分析 先利用勾股定理求得AB的长,然后由翻折的性质可知DF=DB,由DF∥BC可知△AFD∽△ACB,利用相似三角形的性质列出方程求解即可.
解答 解:在Rt△ABC中,由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
由翻折的性质可知:DF=DB.
设BD=x,则DF=x.
∵DF∥BC,
∴△AFD∽△ACB.
∴$\frac{AD}{AB}=\frac{DF}{BC}$,即$\frac{10-x}{10}=\frac{x}{8}$.
解得:x=$\frac{40}{9}$.
故选:A.
点评 本题主要考查的是相似三角形的性质和判定、翻折的性质、勾股定理的应用,利用相似三角形的性质列出关于x的方程是解题的关键.

练习册系列答案
相关题目
1.以边长为1的正方形ABCD的顶点A为圆心,以$\sqrt{2}$为半径作⊙A,则点C关于⊙A的位置关系是( )
| A. | 点C 在⊙A内 | B. | 点C在⊙A上 | C. | 点C在⊙A外 | D. | 不能确定 |
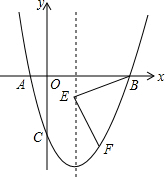 如图所示,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,E为x轴下方的对称轴上一点且EF⊥BE交抛物线于F,且EB=EF,求点F坐标.
如图所示,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,E为x轴下方的对称轴上一点且EF⊥BE交抛物线于F,且EB=EF,求点F坐标.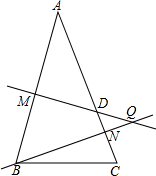 如图,在△ABC中,△ABC中,∠ABC=∠C,AB的垂直平分线MQ交AC于D,CD的垂直平分线恰好过点B,求∠A的度数.
如图,在△ABC中,△ABC中,∠ABC=∠C,AB的垂直平分线MQ交AC于D,CD的垂直平分线恰好过点B,求∠A的度数.